题目内容
【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且CF∥AD.
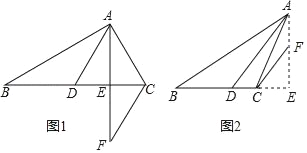
(1)如图1,若△ABC是锐角三角形,∠B=30°,∠ACB=70°,则∠CFE= 度;
(2)若图1中的∠B=x,∠ACB=y,则∠CFE= ;(用含x、y的代数式表示)
(3)如图2,若△ABC是钝角三角形,其他条件不变,则(2)中的结论还成立吗?请说明理由.
【答案】(1)20;(2)![]() y﹣
y﹣![]() x;(3)(2)中的结论成立.
x;(3)(2)中的结论成立.
【解析】
(1)求∠CFE的度数,求出∠DAE的度数即可,只要求出∠BAE-∠BAD的度数,由平分和垂直易得∠BAE和∠BAD的度数即可;
(2)由(1)类推得出答案即可;
(3)类比以上思路,把问题转换为∠CFE=90°-∠ECF解决问题.
解:(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°﹣∠B﹣∠ACB=80°,
∵AD平分∠BAC,
∴∠BAD=40°,
∵AE⊥BC,
∴∠AEB=90°
∴∠BAE=60°
∴∠DAE=∠BAE﹣∠BAD=60°﹣40°=20°,
∵CF∥AD,
∴∠CFE=∠DAE=20°;
故答案为:20;
(2)∵∠BAE=90°﹣∠B,∠BAD=![]() ∠BAC=
∠BAC=![]() (180°﹣∠B﹣∠BCA),
(180°﹣∠B﹣∠BCA),
∴∠CFE=∠DAE=∠BAE﹣∠BAD=90°﹣∠B﹣![]() (180°﹣∠B﹣∠BCA)=
(180°﹣∠B﹣∠BCA)=![]() (∠BCA﹣∠B)=
(∠BCA﹣∠B)=![]() y﹣
y﹣![]() x.
x.
故答案为:![]() y﹣
y﹣![]() x;
x;
(3)(2)中的结论成立.
∵∠B=x,∠ACB=y,
∴∠BAC=180°﹣x﹣y,
∵AD平分∠BAC,
∴∠DAC=![]() ∠BAC=90°﹣
∠BAC=90°﹣![]() x﹣
x﹣![]() y,
y,
∵CF∥AD,
∴∠ACF=∠DAC=90°﹣![]() x﹣
x﹣![]() y,
y,
∴∠BCF=y+90°﹣![]() x﹣
x﹣![]() y=90°﹣
y=90°﹣![]() x+
x+![]() y,
y,
∴∠ECF=180°﹣∠BCF=90°+![]() x﹣
x﹣![]() y,
y,
∵AE⊥BC,
∴∠FEC=90°,
∴∠CFE=90°﹣∠ECF=![]() y﹣
y﹣![]() x.
x.

【题目】为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示.
分组 | 频数 |
4.0≤x<4.2 | 2 |
4.2≤x<4.4 | 3 |
4.4≤x<4.6 | 5 |
4.6≤x<4.8 | 8 |
4.8≤x<5.0 | 17 |
5.0≤x<5.2 | 5 |

(1)求所抽取的学生人数;
(2)若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.