题目内容
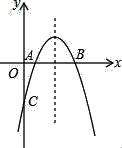
【题目】在平面直角坐标系xOy中，对称轴为直线x=1的抛物线y=﹣x2+bx+c与x轴交于点A和点B，与y轴交于点C，且点B的坐标为（﹣1，0）
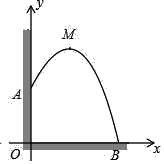
(1)求抛物线的解析式并作出图象；
(2)点D的坐标为（0，1），点P是抛物线上的动点，若△PCD是以CD为底的等腰三角形，求点P的坐标．
【答案】(1) y=﹣x2+2x+3，画图象见解析； (2)点P的坐标为（1+
，2）或（1﹣，2）．
【解析】
（1）求出A、B坐标，利用待定点C的坐标为（0，3），点D（1，0），
（2）由点C的坐标为（0，3），点D（1，0），可知满足条件的点P的纵坐标为2，解方程-x2+2x+3=2即可得到点P的横坐标，由此即可解决问题．
解：（1）
∵抛物线的对称轴为直线x=1，y=﹣x2+bx+c与x轴交于点A和点B，
∴由题意可求点A的坐标为（3，0）．
将点A（3，0）和点B（﹣1，0）代入y=﹣x2+bx+c，
得
，
解得
，
∴抛物线的解析式y=﹣x2+2x+3．
∴抛物线和y轴交点坐标为（0，3），
函数图象如图所示：
（2）如图，
∵点C的坐标为（0，3），点D（1，0），
∴满足条件的点P的纵坐标为2．
∴﹣x2+2x+3=2．
解得 x1=1+，x2=1﹣ ，
∴点P的坐标为（1+，2）或（1﹣，2）．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
