题目内容
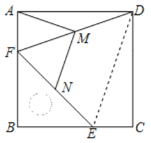
【题目】如图,AB=AC,AB的垂直平分线MN交AC于点D,若∠A=36°,则下列结论:①∠C=72°;②BD是∠ABC的平分线;③△ADB是等腰三角形;④△BCD的周长=AB+BC.正确是______(填序号).
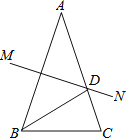
【答案】①②③④
【解析】
①,△ABC中,∠A=36°,AB=AC,根据等腰三角形的性质与三角形内角和定理,即可求得∠C的度数;
对于②,分别求出∠ABD与∠DBC的度数,便可判断BD是否是∠ABC的平分线;
对于③,由线段垂直平分线的性质,得到AD=BD,即可判断△ABD的形状;
对于④,由AD=BD,AC=AB,根据三角形的周长周长公式及线段间的等量代换即可得△BCD的周长.
∵ AB=AC,
∴ ∠ABC=∠ACB.
∵ ∠BAC=36°,
∴ ∠ABC=∠ACB=72° .
故①正确;
∵ MN垂直平分AB,
∴ AD=BD,
∴ △ABD是等腰三角形,
∴ ∠BAC=∠ABD=36° .
∵ ∠ABD=36°,∠ABC=72°,
∴ ∠DBC=36°,
∴ BD平分∠ABC.
故②③正确;
∵ AD=BD,
∴ △BCD的周长=BD+CD+BC=AD+DC+BC=AC+BC.
∵ AC=AB,
∴ △BCD的周长=AB+BC.
故④正确.
综上可知,结论中成立的有①②③④.

练习册系列答案
相关题目
【题目】张明、王成两位同学在初二学年10次数学单元检测的成绩(成绩均为整数,且个位数为0)如图所示利用图中提供的信息,解答下列问题:
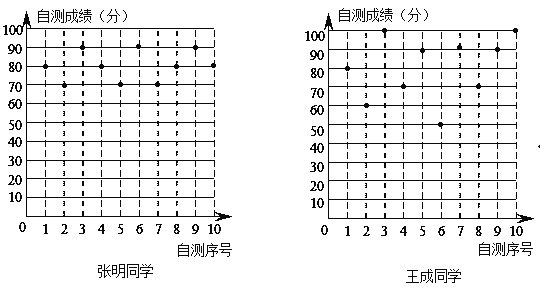
(1)完成下表:
姓名 | 平均成绩 | 中位数 | 众数 | 方差(s2) |
张明 |
| 80 | 80 |
|
王成 |
|
|
| 260 |
(2)如果将90分以上(含90分)的成绩视为优秀,则优秀率较高的同学是 ;
(3)根据图表信息,请你对这两位同学各提出学习建议.