题目内容
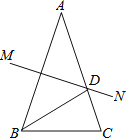
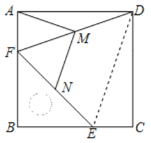
【题目】如图,把一个含45°角的直角三角尺BEF和个正方形ABCD摆放在起,使三角尺的直角顶点和正方形的顶点B重合,连接DF,DE,M,N分别为DF,EF的中点,连接MA,MN,下列结论错误的是( )
A. ∠ADF=∠CDEB. △DEF为等边三角形
C. AM=MND. AM⊥MN
【答案】B
【解析】
连接DE,先根据直角三角形的性质得出AM=![]() DF,再根据△BEF是等腰直角三角形得出AF=CE,由SAS定理得出△ADF≌△CDE,可得∠ADF=∠CDE ,DE=DF,再根据点M,N分别为DF,EF的中点,得出MN是△EFD的中位线,故MN=
DF,再根据△BEF是等腰直角三角形得出AF=CE,由SAS定理得出△ADF≌△CDE,可得∠ADF=∠CDE ,DE=DF,再根据点M,N分别为DF,EF的中点,得出MN是△EFD的中位线,故MN=![]() DE,MN∥DE,可得AM=MN,由MN∥DE,可得∠FMN=∠FDE,根据三角形外角性质可得∠AMF=2∠ADM,由∠ADM+∠DEC+∠FDE=∠FMN+∠AMF=90°,可得MA⊥MN,只能得到△DEF是等腰三角形,无法得出是等边三角形,据此即可得出结论.
DE,MN∥DE,可得AM=MN,由MN∥DE,可得∠FMN=∠FDE,根据三角形外角性质可得∠AMF=2∠ADM,由∠ADM+∠DEC+∠FDE=∠FMN+∠AMF=90°,可得MA⊥MN,只能得到△DEF是等腰三角形,无法得出是等边三角形,据此即可得出结论.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAD=∠C=90°,
∵点M是DF的中点,
∴AM=![]() DF,
DF,
∵△BEF是等腰直角三角形,
∴BF=BE,
∴AF=CE,
∴△ADF≌△CDE(SAS),
∴∠ADF=∠CDE ,DE=DF,
∵点M,N分别为DF,EF的中点,
∴MN是△EFD的中位线,
∴MN=![]() DE,
DE,
∴AM=MN;
∵MN是△EFD的中位线,
∴MN∥DE,
∴∠FMN=∠FDE,
∵AM=MD,
∴∠MAD=∠ADM,
∵∠AMF是△ADM外角,
∴∠AMF=2∠ADM.
又∵∠ADM=∠DEC,
∴∠ADM+∠DEC+∠FDE=∠FMN+∠AMF=90°,
∴MA⊥MN,
∵DE=DF,
∴△DEF是等腰三角形,无法得出是等边三角形,
综上,A、C、D正确,B错误,
故选B.

练习册系列答案
相关题目