题目内容
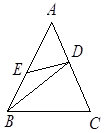
在△ABC中,AD是高,在线段DC上取一点E,使BD=DE,已知AB+BD=DC,
求证:E点在线段AC的垂直平分线上。
求证:E点在线段AC的垂直平分线上。

证明:∵AD是高, ∴ AD⊥BC,
又 BD=DE
∴ AD所在的直线是线段BE的垂直平分线
∴AB=AE ……………………6分
于是 AB+BD=AE+DE
又 AB+BD=DC
∴ DC=AE+DE 即 DE+EC=AE+DE
∴ EC=AE
∴ 点E在线段AC的垂直平分线上
又 BD=DE
∴ AD所在的直线是线段BE的垂直平分线
∴AB=AE ……………………6分
于是 AB+BD=AE+DE
又 AB+BD=DC
∴ DC=AE+DE 即 DE+EC=AE+DE
∴ EC=AE
∴ 点E在线段AC的垂直平分线上
此题考查三角形中垂直平分线
证明:∵AD是高, ∴ AD⊥BC,
又 BD=DE
∴ AD所在的直线是线段BE的垂直平分线
∴AB=AE
于是 AB+BD=AE+DE
又 AB+BD=DC
∴ DC=AE+DE 即 DE+EC=AE+DE
∴ EC=AE
∴ 点E在线段AC的垂直平分线上
点评:垂直平分线上的点到线段两段的距离相等。
证明:∵AD是高, ∴ AD⊥BC,
又 BD=DE
∴ AD所在的直线是线段BE的垂直平分线
∴AB=AE
于是 AB+BD=AE+DE
又 AB+BD=DC
∴ DC=AE+DE 即 DE+EC=AE+DE
∴ EC=AE
∴ 点E在线段AC的垂直平分线上
点评:垂直平分线上的点到线段两段的距离相等。

练习册系列答案
相关题目