题目内容
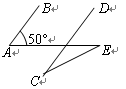
如图，AB∥CD，用含α、β、γ的式子表示θ，则θ=（ ）
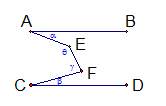
| A．α+γ-β | B．β+γ-α | C．180°+γ-α-β | D．180°+α+β-γ |
D
分析：过点E作EM∥AB，过点F作FN∥CD，由平行线性质可得各角关系求解．
解答：解：过点E作EM∥AB，过点F作FN∥CD，
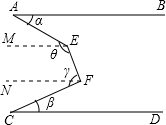
由平行线的传递性得，AB∥EM∥NF∥CD，
∵EM∥AB，
∴∠α=∠AEM，
∵FN∥CD，
∴∠β=∠CFN，
∵EM∥FN，
∴∠MEF+∠EFN=180°，
又∠θ=∠AEM+∠MEF=∠α+180°-（∠γ-∠β）=180°+∠α+∠β-∠γ．
故选D．
解答：解：过点E作EM∥AB，过点F作FN∥CD，
由平行线的传递性得，AB∥EM∥NF∥CD，
∵EM∥AB，
∴∠α=∠AEM，
∵FN∥CD，
∴∠β=∠CFN，
∵EM∥FN，
∴∠MEF+∠EFN=180°，
又∠θ=∠AEM+∠MEF=∠α+180°-（∠γ-∠β）=180°+∠α+∠β-∠γ．
故选D．
练习册系列答案
相关题目
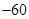米，此时小明的位置在( )
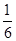，则这个角的度数为 ______．
