题目内容
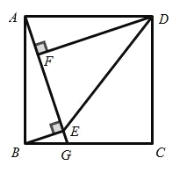
【题目】如图,已知正方形ABCD的边长为12,E是BC中点,将正方形边CD沿DE折叠到DF,将AD折叠,使AD与DF重合,折痕交AB于G,连接BF,CF,则下列结论:①G、F、E三点共线;②BG=8;③△BEF∽△CDF;④S△BFG=![]() .其中正确的有( )
.其中正确的有( )
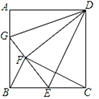
A. ①② B. ①②③ C. ②③④ D. ①②③④
【答案】D
【解析】分析:根据已知条件易证∠GFD+∠DFE=180°,即可得点G、F、E共线,①正确;设BG=x,则GF=AG=12-x,Rt△BEG中根据勾股定理求得x的值,即可判定②正确;根据折叠的性质和已知条件证得∠CDF=∠BEF,再由BE=FE,FD=CD,即可判定△BEF∽△CDF,③正确;在Rt△BEG中,根据面积法可得EG边上的高为![]() ,根据三角形的面积公式即可求得S△BFG=
,根据三角形的面积公式即可求得S△BFG=![]() ,④正确.
,④正确.
详解:由题意得∠GFD=∠DFE=90°,
∴∠GFD+∠DFE=180°,故点G、F、E共线,故①正确;
设BG=x,则GF=AG=12-x,
由题意得:EF=CE=BE=6,
在Rt△BEG中,有BG2+BE2=EG2,
![]()
解得x=8,故②正确;
在四边形DCEF中,
∵∠DFE=∠DCE=90°,
∴∠CEF+∠CDF=180°,
又∠CEF+∠BEF=180°,
∴∠CDF=∠BEF,
∵BE=FE,FD=CD,
∴△BEF∽△CDF,故③正确;
在Rt△BEG中,根据面积法可得EG边上的高为![]() ,又FG=4,∴S△BFG=
,又FG=4,∴S△BFG=![]() ,故④正确;
,故④正确;
所以正确的有①②③④,故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目