题目内容
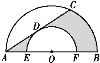
【题目】如图,AB是半圆O的直径,以O为圆心,OE长为半径的小半圆交AB于E,F两点,弦AC是小半圆的切线,D为切点,已知AO=4,EO=2,那么阴影部分的面积是__.
【答案】4![]() +
+![]() π.
π.
【解析】
连接OD、OC,根据切线的性质可得OD⊥AC;已知EO=DO=2,OA=OC=4,由此可得∠OAD=∠OCD=30°,AD=CD;根据直角三角形两锐角互余求得∠AOD=∠COD=60°,由平角的定义求得∠COB=60°;在Rt△OAD中,由勾股定理求得AD=2![]() ,即可得AC=4
,即可得AC=4![]() , 根据S阴影=S△AOC+S扇形BOC-S小半圆即可解答.
, 根据S阴影=S△AOC+S扇形BOC-S小半圆即可解答.
如图,连接OD,OC,则OD⊥AC,
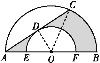
因为EO=DO=2,OA=OC=4,
所以∠OAD=∠OCD=30°,AD=CD,
所以∠AOD=∠COD=60°,
所以∠COB=180°-60°-60°=60°.
在Rt△OAD中,由勾股定理得AD=2![]() ,
,
所以AC=4![]() ,
,
S阴影=![]() ×4
×4![]() ×2+
×2+![]() π×42-
π×42-![]() π×22=4
π×22=4![]() +
+![]() π.
π.

练习册系列答案
相关题目