Question

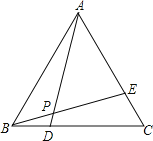
【题目】如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形。把它们沿图中虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为多少cm（ ）

A. 124B. 144C. 110D. 94

Answer 1

【答案】B

【解析】

由题意得出△ABC为等边三角形，△OPQ为等边三角形，得出∠A=∠B=∠C=60°，AB=BC=AC．∠POQ=60°，连结AO，作QM⊥OP于M，在Rt△AOD中，∠OAD=∠OAK=30°，得出OD的长，求出OP，无盖柱形盒子的容积=底面积×高，即可得出结果．

如图由题意得：△ABC为等边三角形，△OPQ为等边三角形，AD=AK=BE=BF=CG=CH=4cm，

∴∠A=∠B=∠C=60°,AB=BC=AC,∠POQ=60°,

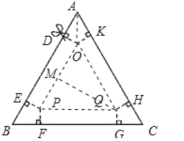
∴∠ADO=∠AKO=90°.

连结AO，作QM⊥OP于M，

在Rt△AOD中,∠OAD=∠OAK=30°，

∴OD=AD=cm，

∵PQ=OP=DE=202×4=12(cm)，

∴QM=OPsin60°=12×=6(cm)，

∴无盖柱形盒子的容积=×12×6×=144()；

故选：B.