Question

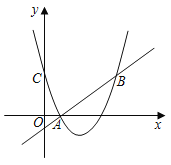
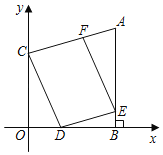
【题目】如图，已知点A（7，8）、C（0，6），AB⊥x轴，垂足为点B，点D在线段OB上，DE∥AC，交AB于点E，EF∥CD，交AC于点F．

（1）求经过A、C两点的直线的表达式；

（2）设OD＝t，BE＝s，求s与t的函数关系式；

（3）是否存在点D，使四边形CDEF为矩形？若存在，请直接写出点D的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y＝x+6；（2）s＝2﹣t（0＜t＜7）；（3）点D的坐标为（，0）．

【解析】

（1）将点A、C的坐标代入一次函数表达式y＝kx+b，即可求解；

（2）根据题意可得点D（t，0），点E（7，s），根据一次函数的图象及性质，可得直线DE的表达式为：y＝x﹣t，将点E的坐标代入即可求解；

（3）设点D（t，0），证明∠OCD＝∠BDE，则tan∠OCD＝tan∠BDE，列出比例式即可求解．

解：（1）设直线AC的表达式为y＝kx+b

将点A、C的坐标代入，得

得：，

解得：，

故直线AC的表达式为：y＝x+6；

（2）∵OD＝t，BE＝s，AB⊥x轴

∴则点D（t，0），点E（7，s）

∵DE∥AC

可设直线DE的解析式为y＝x+c

将点D的坐标代入

0＝t+c

解得：c=﹣t

∴直线的表达式为：y＝x﹣t，

将点E的坐标代入，得s＝2﹣t（根据点D在线段OB上，可得0＜t＜7）；

（3）存在，理由：

设点D（t，0），由（2）BE＝2﹣t，

四边形CDEF为矩形，则∠CDE＝90°，

∵∠EDB+∠CDO＝90°，∠CDO+∠OCD＝90°，

∴∠OCD＝∠BDE，

∴tan∠OCD＝tan∠BDE，

∴＝

即＝，

解得：t＝或7（因为0＜t＜7，故舍去7），

故点D的坐标为（，0）．