Question

【题目】如图，在平面直角坐标系xOy中，一次函数y=﹣2x的图象与反比例函数y=的图象交于点A（﹣1，n）．

（1）求反比例函数y=的解析式；

（2）若P是坐标轴上一点，且满足PA=OA，直接写出点P的坐标．

Answer 1

【答案】（1）y=﹣；（2）点P的坐标为（﹣2，0）或（0，4）．

【解析】

试题分析：（1）先把A（﹣1，n）代入y=﹣2x求出n的值，确定A点坐标为（﹣1，2），然后把A（﹣1，2）代入y=可求出k的值，从而可确定反比例函数的解析式；

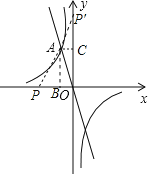
（2）过A作AB⊥x轴于点B，AC⊥y轴于点C，则B点坐标为（﹣1，0），C点坐标为（0，2），由于PA=OA，然后利用等腰三角形的性质易确定满足条件的P点坐标．

解：（1）把A（﹣1，n）代入y=﹣2x得n=﹣2×（﹣1）=2，

∴A点坐标为（﹣1，2），

把A（﹣1，2）代入y=得k=﹣1×2=﹣2，

∴反比例函数的解析式为y=﹣；

（2）过A作AB⊥x轴于点B，AC⊥y轴于点C，如图，

∵点A的坐标为（﹣1，2），

∴B点坐标为（﹣1，0），C点坐标为（0，2）

∴当P在x轴上，其坐标为（﹣2，0）；

当P点在y轴上，其坐标为（0，4）；

∴点P的坐标为（﹣2，0）或（0，4）．