题目内容
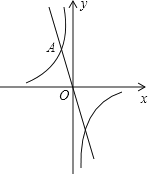
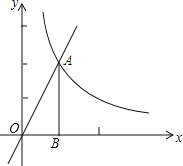
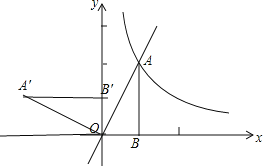
【题目】如图,直线y=2x与双曲线y=![]() 在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )
在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )
A.(2,0) B.(2,﹣1) C.(﹣2,1) D.(﹣1,﹣2)
【答案】C
【解析】
试题分析:通过解方程组![]() 可得A(1,2),则AB=2,OB=1,再根据旋转的性质得AB=A′B′=2,OB=OB′=1,∠A′B′O=∠ABO=90°,∠BOB′=90°,所以点B′在y轴的正半轴上,A′B′⊥y轴,然后利用第二象限点的坐标特征写出A′点的坐标.
可得A(1,2),则AB=2,OB=1,再根据旋转的性质得AB=A′B′=2,OB=OB′=1,∠A′B′O=∠ABO=90°,∠BOB′=90°,所以点B′在y轴的正半轴上,A′B′⊥y轴,然后利用第二象限点的坐标特征写出A′点的坐标.
解:解方程组![]() 得
得![]() 或
或![]() ,则A(1,2),
,则A(1,2),
∵AB⊥x轴,
∴B(1,0),
∴AB=2,OB=1,
∵△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),如图,
∴AB=A′B′=2,OB=OB′=1,∠A′B′O=∠ABO=90°,∠BOB′=90°,
∴点B′在y轴的正半轴上,A′B′⊥y轴,
∴A′点的坐标为(﹣2,1).
故选C.

练习册系列答案
相关题目