题目内容
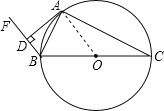
【题目】如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.

(1)求证:AD为⊙O的切线;
(2)若BD=1,tan∠BAD=![]() ,求⊙O的直径.
,求⊙O的直径.
【答案】(1)见解析;(2)5
【解析】
试题分析:(1)要证AD是⊙O的切线,连接OA,只证∠DAO=90°即可.
(2)根据三角函数的知识可求出AD,从而根据勾股定理求出AB的长,根据三角函数的知识即可得出⊙O的直径.
(1)证明:连接OA;
∵BC为⊙O的直径,BA平分∠CBF,AD⊥BF,
∴∠ADB=∠BAC=90°,∠DBA=∠CBA;
∵∠OAC=∠OCA,
∴∠DAO=∠DAB+∠BAO=∠BAO+∠OAC=90°,
∴DA为⊙O的切线.
(2)解:∵BD=1,tan∠BAD=![]() ,
,
∴AD=2,
∴AB=![]() =
=![]() ,
,
∴cos∠DBA=![]() ;
;
∵∠DBA=∠CBA,
∴BC=![]() =
=![]() =5.
=5.
∴⊙O的直径为5.

练习册系列答案
相关题目