题目内容
【题目】如图,AB为⊙O的直径,点C为半圆上一点,AD平分∠CAB交⊙O于点D 
(1)求证:OD∥AC;
(2)若AC=8,AB=10,求AD.
【答案】
(1)证明:∵AD平分∠CAB交⊙O于点D,
∴∠CAD=∠BAD,
∵OA=OD,
∴∠DAB=∠D,
∴∠CAD=∠D,
∴AC∥OD
(2)解:连接BC,BD,
∵AD平分∠CAB交⊙O于点D,
∴ ![]() =
= ![]() ,
,
∴CE=BE,
∵AB为⊙O的直径,
∴∠C=90°,
∴BC= ![]() =6,
=6,
∴CE=BE=3,
∴OE= ![]() =4,
=4,
∴DE=1,
∴BD= ![]() =
= ![]() ,
,
∴AD= ![]() =3
=3 ![]() .
.
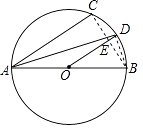
【解析】(1)由AD平分∠CAB交⊙O于点D,得到∠CAD=∠BAD,根据等腰三角形的性质得到∠DAB=∠D,等量代换得到∠CAD=∠D,根据平行线的判定定理即可得到结论;(2)连接BC,BD,根据圆周角定理得到∠C=90°,根据勾股定理即可得到结论.
【考点精析】本题主要考查了圆周角定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目