题目内容
【题目】已知抛物线y=﹣x2+bx+c的部分图象如图所示,A(1,0),B(0,3).
(1)求抛物线的解析式;
(2)结合函数图象,写出当y<3时x的取值范围. 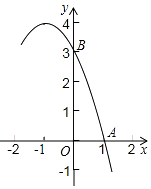
【答案】
(1)解:∵函数的图象过A(1,0),B(0,3),
∴ ![]() ,
,
解得: ![]() .
.
故抛物线的解析式为y=﹣x2﹣2x+3
(2)解:由图象知抛物线的对称轴为x=﹣1,且当y=3时,x=﹣2或0,
故当y<3时x的取值范围为x<﹣2或x>0
【解析】(1)根据函数的图象过A(1,0),B(0,3),再代入y=﹣x2+bx+c,列出方程组,即可求出抛物线的解析式.(2)由抛物线得到对称轴为x=﹣1,得到当y=3时,x=﹣2或0,依此求出相应的x的取值范围即可.
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.).

练习册系列答案
相关题目