题目内容
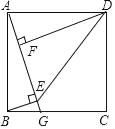
【题目】在Rt△ABC中,∠C=90°,AC=BC,AB=8,点D为AB的中点,若直角MDN绕点D旋转,分别交AC于点E,交BC于F,则下列说法:①AE=CF;②EC+CF=4![]() ;③DE=DF;④若△ECF面积为一个定值,则EF长也是一个定值,其中正确的结论是_____.
;③DE=DF;④若△ECF面积为一个定值,则EF长也是一个定值,其中正确的结论是_____.

【答案】①②③④
【解析】
①如果连接CD,可证△ADE≌△CDF,得出AE=CF;
②由①知,EC+CF=EC+AE=AC,而AC为等腰直角△ABC的直角边,由于斜边AB=8,由勾股定理可求出AC=BC=4![]() ;
;
③由①知DE=DF;
④由△ECF的面积=![]() ×CE×CF,如果这是一个定值,则CECF是一个定值,又EC+CF=
×CE×CF,如果这是一个定值,则CECF是一个定值,又EC+CF=![]() ,从而可唯一确定EC与EF的值,由勾股定理知EF的长也是一个定值.
,从而可唯一确定EC与EF的值,由勾股定理知EF的长也是一个定值.
解:①连接CD.

∵在Rt△ABC中,∠ACB=90°,AC=BC,点D为AB的中点,
∴CD⊥AB,CD=AD=DB,
在△ADE与△CDF中,∠A=∠DCF=45°,AD=CD,∠ADE=∠CDF,
∴△ADE≌△CDF(ASA),
∴AE=CF.
∴①说法正确;
②∵在Rt△ABC中,∠C=90°,AC=BC,AB=8,
∴AC=BC=4![]() .
.
由①知AE=CF,
∴EC+CF=EC+AE=AC=4![]() .
.
∴②说法正确;
③由①知△ADE≌△CDF,
∴DE=DF.
∴③说法正确;
④∵△ECF的面积=![]() ×CE×CF,如果这是一个定值,则CECF是一个定值,
×CE×CF,如果这是一个定值,则CECF是一个定值,
又∵EC+CF=![]() ,
,
∴可唯一确定EC与EF的值,
再由勾股定理知EF的长也是一个定值,
∴④说法正确.
故答案为:①②③④

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目