Question

【题目】如图，点E是菱形ABCD的边AD延长线上的点，AE =AC，CE=CB，则∠B的度数为_______．

Answer 1

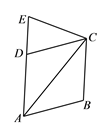
【答案】108 °

【解析】分析：设∠DAC的度数为x，利用菱形的性质得DA=DC，∠DCA=∠DAC=x，则利用三角形外角性质得∠EDC=2x，接着利用等腰三角形的性质得到∠E=∠EDC=2x，∠ACE=∠E=2x，于是利用三角形内角和定理得到x+2x+2x=180°，解得x=36°，然后计算出∠ADC的度数，从而得到∠B的度数．

详解：设∠DAC的度数为x．

∵四边形ABCD为菱形，∴DA=DC，∠ADC=∠B，∴∠DCA=∠DAC=x，∴∠EDC=∠DCA+∠DAC=2x．

∵CD=CE，∴∠E=∠EDC=2x．

∵AE=AC，∴∠ACE=∠E=2x，∴x+2x+2x=180°，解得：x=36°．

∵∠ADC=180°﹣2x=108°，∴∠B=∠ADC=108°．

故答案为：108°．