题目内容
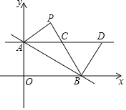
【题目】如图,在△ABC中,AB=AC,∠B=30°,点D从点B出发,沿B→C方向运动到点C(D不与B,C重合),连接AD,作∠ADE=30°,DE交线段AC于点E.设∠B4D=x°,∠AED=y°.
(1)当BD=AD时,求∠DAE的度数;
(2)求y与x的关系式;
(3)当BD=CE时,求x的值.

【答案】解:(1)90°.(2) y=30+x.(3) x=y-30=45.
【解析】
(1)根据等腰三角形的性质得到∠C=∠B=30°,∠BAD=∠B =30°,利用三角形的内角和计算出∠BAC=120°,从而可以计算出∠DAE=90°;
(2)利用三角形的内角和计算出∠BAC=120°,从而∠DAE=120°-x°,利用三角形的内角和表示∠AED=30°+x°,即y=30+x;
(3)先需要证明△ABD≌△DCE,得出AD=DE,从而得出∠DAE=∠AED=y°,利用三角形的内角和计算出y,从而计算出x.
解:(1)∵AB=AC, ∠B=30°,
∴∠C=∠B =30°,
∴∠BAC=180°-∠C-∠B=120°,
∵BD=AD, ∠B=30°,
∴∠BAD=∠B =30°,
∴∠DAE=∠BAC-∠BAD=90°.
(2) ∵AB=AC, ∠B=30°,
∴∠C=∠B =30°,
∴∠BAC=180°-∠C-∠B=120°,
∴∠DAE=∠BAC-∠BAD=120°-x°,
∴∠AED=180°-∠DAE-∠ADE=30°+x°,
即y=30+x.
(3) ∵∠C=30°, ∠AED=30°+x°,
∴∠EDC=∠AED-∠C= x°,
∴∠EDC=∠BAD,
又∵∠C=∠B,
BD=CE,
∴△ABD≌△DCE(AAS),
∴AD=DE,
∴∠DAE=∠AED=y°
∵∠DAE+∠AED+∠ADE=180°
∴2y°+30°=180°
即y°=75°,
∴x=y-30=45.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案