题目内容
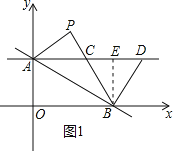
【题目】如图,直线y=kx+8(k<0)交y轴于点A,交x轴于点B.将△AOB关于直线AB翻折得到△APB.过点A作AC∥x轴交线段BP于点C,在AC上取点D,且点D在点C的右侧,连结BD.
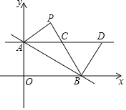
(1)求证:AC=BC
(2)若AC=10.
①求直线AB的表达式.
②若△BCD是以BC为腰的等腰三角形,求AD的长.
(3)若BD平分∠OBP的外角,记△APC面积为S1,△BCD面积为S2,且![]() =
=![]() ,则
,则![]() 的值为______(直接写出答案)
的值为______(直接写出答案)
【答案】(1)证明见解析;(2)①y=-![]() x+8;②20或22;(3)
x+8;②20或22;(3)![]() .
.
【解析】
(1)由平行线的性质可得出∠BAC=∠ABO,由折叠的性质可知∠ABO=∠ABC,进而可得出∠BAC=∠ABC,由等角对等边即可证出AC=BC;
(2)过点B作BE⊥CD于点E.①利用一次函数图象上点的坐标特征可求出OA的长度,进而可得出BE的长度,在Rt△BCE中,利用勾股定理可求出CE的长度,进而可得出OB,AE的长度,由OB的长度可得出点B的坐标,再利用待定系数法即可求出直线AB的表达式;
②分BC=DC及BC=BD两种情况考虑:当BC=DC时,由AC=BC=10,可求出AD的长度;当BC=BD时,利用等腰三角形的性质结合①的结论可求出CD的长度,进而可得出AD的长度.综上,此问得解;
(3)由折叠的性质结合三角形的面积公式可得出![]() ,设PC=2a,则CD=3a,易证△APC≌△BEC(AAS),由全等三角形的性质可得出CE=CP=2a,由角平分线的定义、平行线的性质结合等腰三角形的性质可得出CB=CD=AC=3a,在Rt△BCE中,CE=2a,进而可得出OB=5a,AD=6a,二者相比后即可得出
,设PC=2a,则CD=3a,易证△APC≌△BEC(AAS),由全等三角形的性质可得出CE=CP=2a,由角平分线的定义、平行线的性质结合等腰三角形的性质可得出CB=CD=AC=3a,在Rt△BCE中,CE=2a,进而可得出OB=5a,AD=6a,二者相比后即可得出![]() 的值.
的值.
(1)证明:∵AC∥x轴,
∴∠BAC=∠ABO.
由折叠的性质,可知:∠ABO=∠ABC,
∴∠BAC=∠ABC,
∴AC=BC.
(2)解:过点B作BE⊥CD于点E,如图1所示.
①当x=0时,y=kx+8=8,
∴点A的坐标为(0,8),BE=OA=8.
在Rt△BCE中,BC=AC=10,BE=8,
∴CE=![]() =6,
=6,
∴OB=AE=AC+CE=16,
∴点B的坐标为(16,0).
将点B(16,0)代入y=kx+8,得:0=16k+8,
解得:k=-![]() ,
,
∴直线AB的表达式为y=-![]() x+8.
x+8.
②当BC=DC时,AD=AC+CD=10+10=20;
当BC=BD时,由①可知:CD=2CE=12,
∴AD=AC+CD=10+12=22.
综上:AD的长为20或22.
(3)由折叠的性质,可知:AO=AP,∠APC=∠AOB=90°.
∵S△APC=![]() APPC=
APPC=![]() AOPC,S△BCD=
AOPC,S△BCD=![]() CDAO,OA=BE,
CDAO,OA=BE,
∴![]() =
=![]() ,
,
设PC=2a,则CD=3a.
在△APC和△BEC中,
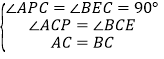 ,
,
∴△APC≌△BEC(AAS),
∴PC=EC.
∵BD平分∠OBP的外角,CD∥x轴,
∴∠CBD=∠CDB,
∴CD=CB=3a.
在Rt△BCE中,CB=3a,CE=2a,
∴BE=![]() =
=![]() a,
a,
∴OB=AC+CE=CD+CE=5a,AD=AC+CD=2CD=6a,
∴![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案