题目内容
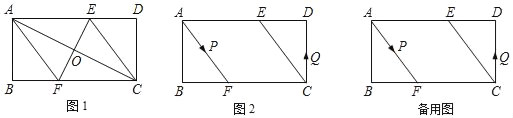
【题目】如图，池塘边有一块长为18米，宽为10米的长方形土地，现在将其中三面留出宽都是x米的小路，中间余下的长方形部分做菜地.
（1）菜地的长a = 米，宽b= 米（用含x的代数式表示）；
（2）菜地的面积S= 平方米（用含x的代数式表示）；
（3）当x=1米时，求菜地的面积．
【答案】（1）18﹣2x，10﹣x；（2）（18﹣2x）（10﹣x）；（3）144m2.
【解析】
本题可先根据所给的图形，得出菜地的长和宽，然后根据长方形面积公式求出面积；第三问可以直接将x=1代入第二问所求的面积式子中，得出结果．
解：（1）∵其余三面留出宽都是x米的小路，
∴由图可以看出：菜地的长为18-2x米，宽为10-x米；
（2）由（1）知：菜地的长为18-2x米，宽为10-x米，
所以菜地的面积为S=（18-2x）（10-x）；
（3）由（2）得菜地的面积为：S=（18-2x）（10-x），
当x=1时，S=（18-2）（10-1）=144m2．
故答案分别为：（1）18﹣2x，10﹣x；（2）（18﹣2x）（10﹣x）；（3）144m2.
练习册系列答案
相关题目
【题目】为节约用水、保护水资源，本市制定了一套节约用水的管理措施，其中规定每月用水量超过m（吨）时，超过部分每吨加收环境保护费 
元．下图反映了每月收取的水费y（元）与每月用水量x（吨）之间的函数关系的图象．按上述方案，一家酒店四、五两月用水量及缴费情况如表：
月份 | 用水量x（吨） | 水费y（元） |
四月 | 35 | 59.5 |
五月 | 80 | 151 |
（1）求出m的值；
（2）写出y与x之间的函数关系式，并指出自变量x的取值范围．
