题目内容
如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8)DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求AC的长;
(3)在图2中,点G是x轴正半轴上一点,且0<OG<4,过G作EF垂直于x轴,分别交y1、y2的图象于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②线段EF长有可能等于3吗?若能,请求出相应的x的值,若不能请说明理由.

(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求AC的长;
(3)在图2中,点G是x轴正半轴上一点,且0<OG<4,过G作EF垂直于x轴,分别交y1、y2的图象于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②线段EF长有可能等于3吗?若能,请求出相应的x的值,若不能请说明理由.

分析:(1)根据∠C=90°,利用直角三角形的面积等于两直角边乘积的一半列式整理即可得解,再利用两点法画出函数图象即可;
(2)根据x=4表示出AP、PC、CQ的长,再根据△PCQ的面积列式求解即可得到k的值,然后根据AC=8k计算即可得解;
(3)①根据函数值y表示出两个三角形的面积,EF表示两个三角形的面积的差;
②根据k值求出y2与x的关系式,然后表示出EF,再令EF=3,解关于x的方程即可.
(2)根据x=4表示出AP、PC、CQ的长,再根据△PCQ的面积列式求解即可得到k的值,然后根据AC=8k计算即可得解;
(3)①根据函数值y表示出两个三角形的面积,EF表示两个三角形的面积的差;
②根据k值求出y2与x的关系式,然后表示出EF,再令EF=3,解关于x的方程即可.
解答: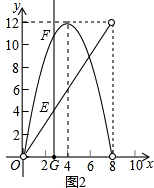 解:(1)∵∠C=90°,
解:(1)∵∠C=90°,
∴S△DCQ=
•CQ•CD=
×3x=
x,
∴y1=
x,
图象如图所示;
(2)∵抛物线的顶点坐标是(4,12),
∴当x=4时,△PCQ面积为12,
此时,AP=4k,
PC=AC-AP=8k-4k=4k,
CQ=4,
∴S△PCQ=
CQ•PC=12,
即
×4×4k=12,
解得k=
,
所以,点P的速度每秒
厘米,
所以,AC=8×
=12厘米;
(3)①观察图象,知线段的长EF=y2-y1,
表示△PCQ与△DCQ的面积差(或△PDQ面积);
②y2=
PC•CQ=
(12-
x)•x=-
x2+6x,
∵EF=y2-y1,
∴EF=-
x2+6x-
x=-
x2+
x,
假设EF=3,则-
x2+
x=3,
整理得,x2-6x+4=0,
解得x1=3+
,x2=3-
,
∵0<OG<4,
∴0<x<4,
∴x=3-
,
故当x=3-
时,EF=3.
 解:(1)∵∠C=90°,
解:(1)∵∠C=90°,∴S△DCQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴y1=
| 3 |
| 2 |
图象如图所示;
(2)∵抛物线的顶点坐标是(4,12),
∴当x=4时,△PCQ面积为12,
此时,AP=4k,
PC=AC-AP=8k-4k=4k,
CQ=4,
∴S△PCQ=
| 1 |
| 2 |
即
| 1 |
| 2 |
解得k=
| 3 |
| 2 |
所以,点P的速度每秒
| 3 |
| 2 |
所以,AC=8×
| 3 |
| 2 |
(3)①观察图象,知线段的长EF=y2-y1,
表示△PCQ与△DCQ的面积差(或△PDQ面积);
②y2=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
∵EF=y2-y1,
∴EF=-
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 2 |
假设EF=3,则-
| 3 |
| 4 |
| 9 |
| 2 |
整理得,x2-6x+4=0,
解得x1=3+
| 5 |
| 5 |
∵0<OG<4,
∴0<x<4,
∴x=3-
| 5 |
故当x=3-
| 5 |
点评:本题是二次函数综合题型,主要考查了三角形的面积,作一次函数的图象,二次函数的性质,以及函数图象上平行于y轴的两点间的距离的表示方法,综合题,但难度不大,理清点P、Q的运动过程中两个三角形的直角边的表示是解题的关键.

练习册系列答案
相关题目