题目内容
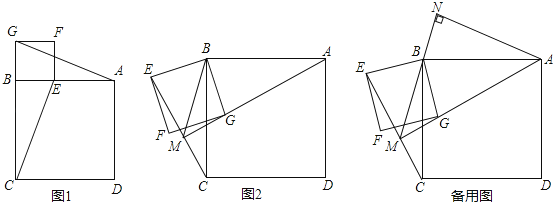
【题目】(1)如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,求证:![]() =
=![]() .
.
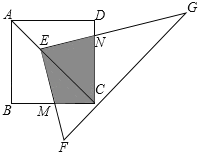
(2)如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若![]() ,则
,则![]() 的值为 .
的值为 .
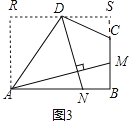
(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=12,BC=CD=4,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,易证AP=EF,GH=BQ,△PDA∽△QAB,然后运用相似三角形的性质就可解决问题;
(2)只需运用(1)中的结论,就可得到![]() ,就可解决问题;
,就可解决问题;
(3)过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图3,易证四边形ABSR是矩形,由(1)中的结论可得![]() .设SC=x,DS=y,则AR=BS=4+x,RD=12-y,在Rt△CSD中根据勾股定理可得x2+y2=16①,在Rt△ARD中根据勾股定理可得(4+x)2+(12-y)2=144②,解①②就可求出x,即可得到AR,问题得以解决.
.设SC=x,DS=y,则AR=BS=4+x,RD=12-y,在Rt△CSD中根据勾股定理可得x2+y2=16①,在Rt△ARD中根据勾股定理可得(4+x)2+(12-y)2=144②,解①②就可求出x,即可得到AR,问题得以解决.
解:(1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,
∵四边形ABCD是矩形,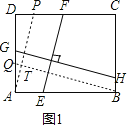
∴AB∥DC,AD∥BC.
∴四边形AEFP、四边形BHGQ都是平行四边形,
∴AP=EF,GH=BQ.
又∵GH⊥EF,
∴AP⊥BQ,
∴∠QAT+∠AQT=90°.
∵四边形ABCD是矩形,
∴∠DAB=∠D=90°,
∴∠DAP+∠DPA=90°,
∴∠AQT=∠DPA.
∴△PDA∽△QAB,
∴![]() ,
,
∴![]() =
=![]() .
.
(2)如图2,
∵EF⊥GH,AM⊥BN,
∴由(1)中的结论可得![]() =
=![]() ,
,![]() =
=![]() ;
;
∴![]() ,
,
故答案为![]() ;
;
(3)过点D作平行于AB
则四边形ABSR是平行四边形.
∵∠ABC=90°,
∴平行四边形ABSR是矩形,
∴∠R=∠S=90°,RS=AB=12,AR=BS.
∵AM⊥DN,
∴由(1)中的结论可得 ![]() .
.
设SC=x,DS=y,则AR=BS=4+x,RD=12﹣y,
∴在Rt△CSD中,x2+y2=16①,
在Rt△ARD中,(4+x)2+(12﹣y)2=144②,
由②﹣①得x=3y﹣4③,
解方程组 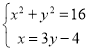 ,得
,得![]() (舍去),或
(舍去),或 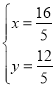 ,
,
∴AR=4+x=![]()
∴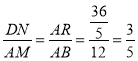 .
.