题目内容
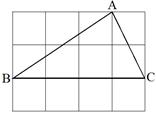
如图正方形网格中的△ABC,若小方格边长为1,请你根据所学的知
(1)求△ABC的面积
(2)判断△ABC是什么形状? 并说明理由.
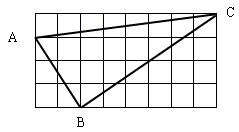
(1)求△ABC的面积
(2)判断△ABC是什么形状? 并说明理由.

(1)13;(2)直角三角形;理由见解析.
试题分析:(1)用长方形的面积减去三个小三角形的面积即可求出△ABC的面积.
(2)根据勾股定理求得△ABC各边的长,再利用勾股定理的逆定理进行判定,从而不难得到其形状.
试题解析:(1)△ABC的面积=4×8-1×8÷2-2×3÷2-6×4÷2=13.
故△ABC的面积为13;
(2)∵正方形小方格边长为1
∴AC=
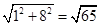 ,AB=
,AB=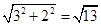 ,BC=
,BC=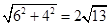 ,
,∵在△ABC中,AB2+BC2=13+52=65,AC2=65,
∴AB2+BC2=AC2,
∴网格中的△ABC是直角三角形.

练习册系列答案
相关题目

 ,如图1所示,将△
,如图1所示,将△ 与点A重合,并绕点A按逆时针方向旋转,使点D,A(
与点A重合,并绕点A按逆时针方向旋转,使点D,A( = ° ,与BC相等的线段是 。
= ° ,与BC相等的线段是 。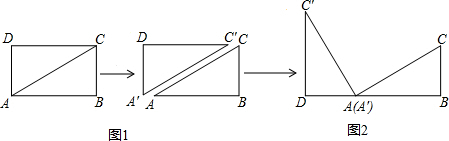

 ,求
,求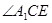 的度数。
的度数。