题目内容
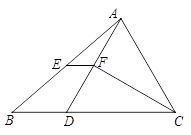
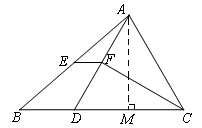
如图,△ABC中,BC >AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.
(1)求证:EF∥BD ;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.
(1)求证:EF∥BD ;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.

(1)证明见解析;(2)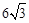 .
.
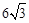 .
.试题分析:(1)由题意可推出△ADC为等腰三角形,CF为顶角的角平分线,所以也是底边上的中线和高,因此F为AD的中点,所以EF为△ABD的中位线,即EF∥BD.
(2)根据(1)的结论,可以推出△AEF∽△ABD,且S△AEF:S△ABD=1:4,所以S△AEF:S四边形BDEF=1:3,即可求出△AEF的面积,从而由
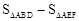 求得四边形BDFE的面积.
求得四边形BDFE的面积.(1)∵ CA=CD,CF平分∠ACB,∴ CF是AD边的中线.
∵ E是AB的中点,∴ EF是△ABD的中位线.
∴ EF∥BD .
(2)∵∠ACB=60°,CA=CD,∴△CAD是等边三角形.
∴∠ADC=60°,AD=DC=AC=8.∴ BD=BC-CD=4.
如图,过点A作AM⊥BC,垂足为M .
∴
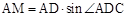
 .
.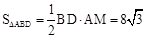 .
.∵ EF∥BD ,∴△AEF ∽△ABD ,且
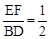 .
.∴
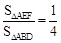 .∴
.∴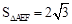 .
. 四边形BDFE的面积=
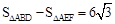 .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目


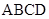 中,
中,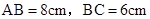 ,点
,点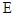 是
是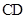 的中点,动点
的中点,动点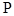 从
从 点出发,以每秒
点出发,以每秒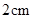 的速度沿
的速度沿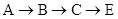 运动,最终到达点
运动,最终到达点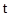 秒,那么当
秒,那么当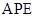 的面积会等于10 ?
的面积会等于10 ?