Question

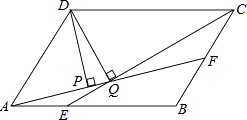
【题目】如图1，在矩形ABCD中，AC为对角线，延长CD至点E使CE=CA，连接AE。F为AB上一点，且BF=DE，连接FC.

（1）若DE=1，CF=2，求CD的长。

（2）如图2，点G为线段AE的中点，连接BG交AC于H，若∠BHC+∠ABG=600，求证：AF+CE=AC.

Answer 1

【答案】（1）3；（2）见解析.

【解析】分析：（1）先证明△ADE≌△CBF，可得AE=CF= ，设CD=x，则CE=AC=x+1 ，在Rt△ACD中根据勾股定理列方程求解；

（2）延长BG交CD的延长线于点M，先证明△ABG≌EMG，从而可得CE+AF= 2CD，由等腰三角形的性质和三角形外角的性质可求∠M=∠MCG=∠ACG=∠ABG=15°，从而∠ACD=30，由cos∠ACD=得,进而可证明结论.

详解：(1)解：∵矩形ABCD ，

∴AD=BC，∠ADC=∠ABC=90 .

∵∠ADE+∠ADC=180 ，

∴∠ADC=90 ，

∴∠ADC=∠ABC .

∵BF=DE ，

∴△ADE≌△CBF ，

∴AE=CF= ，

∴在Rt△ABC中，

AD= ，

设CD=x，则CE=AC=x+1 ，

，

解得： ，

即： ；

(2)证明：延长BG交CD的延长线于点M

易证△ABG≌EMG，

∴GM=GB,AB=CD,∠ABG=∠M，

又BF=ED，

∴AF=ME.

∴CE+AF=CE+ME=2CD,

连接CG, 在Rt△MCB，

CG=MG，

∴∠M=∠MCG.

又CA=CE，且点G是AE的中点,

∴ ∠MCG=∠ACG,

又∠BHC=∠M+∠MCG+∠ACG, ∠BHC+∠ABG=60,

∴∠M=∠MCG=∠ACG=∠ABG=15

∴∠ACD=30

∵cos∠ACD=,

∴,

∴AF+CE=AC.