题目内容
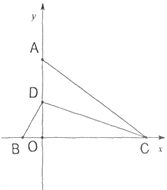
【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB,与y轴交于D点,∠CAO=90°-∠BDO.
(1)求证:AC=BC:
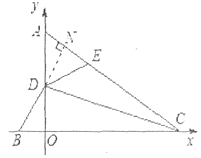
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;

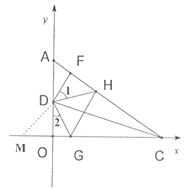
(3)如图3,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,当H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
 (图3)
(图3)
【答案】(1)证明见解析;(2)8;(3)GH=FH+OG,证明见解析.
【解析】试题分析: (1)由题意∠CAO=90°-∠BDO,可知∠CAO=∠CBD,CD平分∠ACB与y轴交于D点,所以可由AAS定理证明△ACD≌△BCD,由全等三角形的性质可得AC=BC;
(2)过D作DN⊥AC于N点,可证明Rt△BDO≌Rt△EDN、△DOC≌△DNC,因此,BO=EN、OC=NC,所以,BC+EC=BO+OC+NC-NE=2OC,即可得BC+EC的长;
(3)在x轴的负半轴上取OM=FH,可证明△DFH≌△DOM、△HDG≌△MDG,因此,MG=GH,所以,GH=OM+OG=FH+OG,即可证明所得结论.
试题解析:
(1)证明:∵∠CAO=90°-∠BDO,
∴∠CAO=∠CBD.
又∵∠ACD=∠BCD,CD=CD,
∴△ACD≌△BCD(AAS).
∴AC=BC.
(2)解:过D作DN⊥AC于N点,如图所示:
∵∠ACD=∠BCD,∠DOC=∠DNC=90°,
CD=CD
∴△DOC≌△DNC(AAS),
∴DO=DN,OC=NC.
又∵∠DEA=∠DBO,∠DOB=∠DNC=90°
∴△BDO≌△EDN(AAS),
∴BO=EN.
∴BC+EC=BO+OC+NC-NE=2OC=8.
(3)GH=FH+OG.
证明:由(1)知:DF=DO,
在x轴的负半轴上取OM=FH,连接DM,
如图所示:
在△DFH和△DOM中
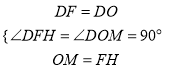
∴△DFH≌△DOM(SAS).
∴DH=DM,∠l=∠ODM.
∴∠GDH=∠1+∠2=∠ODM+∠2=∠GDM.
在△HDG和△MDG中
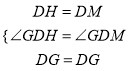
∴△HDG≌△MDG(SAS).
∴MG=GH,
∴GH=OM+OG=FH+OG.
点睛: 本题主要考查了全等三角形的判定及其性质,做题时添加了辅助线,正确作出辅助线是解决问题的关键.

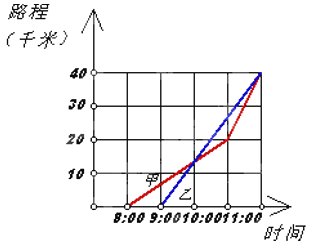
【题目】某校九年级两个班,各选派10名学生参加学校举行的“数学奥林匹克”大赛预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | 94 | b | 93 | 12 |
九(2)班 | 99 | a | 95.5 | 93 | 8.4 |
(1)直接写出表中a、b的值:a= , b=;
(2)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.