Question

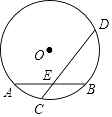
【题目】如图，平行四边形ABCD中，AB：BC=3：2，∠DAB=60°，E在AB上，且AE：EB=1：2，F是BC的中点，过D分别作DP⊥AF于P，DQ⊥CE于Q，则DP：DQ等于（ ）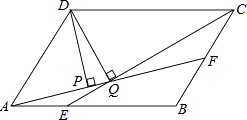

A.3：4
B. ：2
C. ：2
D.2 ：

Answer 1

【答案】D
【解析】解：连接DE、DF，过F作FN⊥AB于N，过C作CM⊥AB于M，

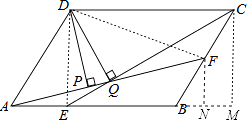
∵根据三角形的面积和平行四边形的面积得：S△DEC=S△DFA= S平行四边形ABCD，

即 AF×DP= CE×DQ，

∴AF×DP=CE×DQ，

∵四边形ABCD是平行四边形，

∴AD∥BC，

∵∠DAB=60°，

∴∠CBN=∠DAB=60°，

∴∠BFN=∠MCB=30°，

∵AB：BC=3：2，

∴设AB=3a，BC=2a，

∵AE：EB=1：2，F是BC的中点，

∴BF=a，BE=2a，

BN= a，BM=a，

由勾股定理得：FN= a，CM= a，

AF= = a，

CE= =2 a，

∴ aDP=2 aDQ

∴DP：DQ=2 ： ．

故答案为：D．

连接DE、DF，过F作FN⊥AB于N，过C作CM⊥AB于M，得出根据三角形的面积和平行四边形的面积得：S△DEC=S△DFA= S平行四边形ABCD，证得AF×DP=CE×DQ，由AB：BC=3：2，AE：EB=1：2，F是BC的中点，设AB=3a，用含a的代数式分别表示出BC、BF、BE、BN、BM的长，利用勾股定理求出AF、CE的长，代入AF×DP=CE×DQ，即可求出DP：DQ的值。