题目内容
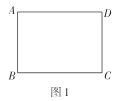
【题目】如图1，在平面直角坐标系中Rt△AOB≌Rt△DCA，其中B（0，4），C（2，0）．连接BD．
（1）求直线BD的解析式；
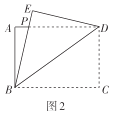
（2）点E是直线AD上一点，连接BE，以BE，ED为一组邻边作BEDF，当BEDF的面积为3时，求点E的坐标；
（3）如图2，将△DAC沿x轴向左平移，平移距离大于0，记平移后的△DAC为△D′A′C′，连接D′A，D′B，当△D′AB为等腰三角形时，直接写出点D′的坐标．
【答案】（1）直线BD的表达式为：y＝﹣x+4；（2）点E的坐标为（1，
）或（3，
）；（3）点D′的坐标为（﹣6，2）或（﹣4，2）．
【解析】
（1）
，则AO=CD，OB=AC=4，
，则点
，即可求解；
（2）设直线
交
轴于点
，则点
，利用
，即可求解；
（3）分
、
、
，求解即可．
解：（1）
，
，
，
，
点，
将
、
坐标代入一次函数：
得：
，解得：
，
故直线
的表达式为：
，
同理直线的表达式为：
；
（2）①当点
在线段上时，
设直线交轴于点，则点，
，
即：
，
解得：
，即点
，
②当点在线段外时，
同理可得：点
，
故点的坐标为
或
；
（3）设图象向左平移
个单位，则点
，
则：
，
，
，
当时，即：
，
解得：
，
刚好是在线段
上，所以形成不了三角形，故舍去；
当时，同理可得：
，
当时，同理可得：
，
故：点的坐标为
或
．
练习册系列答案
相关题目
