Question

【题目】综合与实践

问题情境

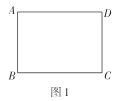
综合与实践课上，老师让同学们以“折纸”为主题开展数学活动．如图1，有一张长为4，宽为3的矩形纸片（）．

操作发现

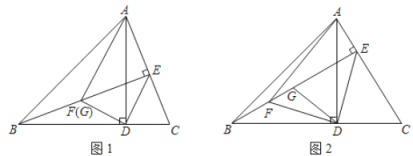
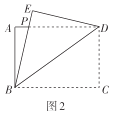
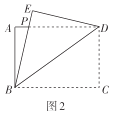
（1）快乐小组先将图1中的矩形纸片沿直线折叠，使得点落在点处，得到图2，他们发现，请你证明这个结论；

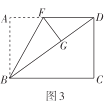
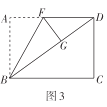
（2）创新小组将图2中的矩形纸片展开后继续折叠，使得点落在对角线上的点处，折痕为，得到图3，则折痕__________；

实践探究

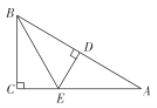
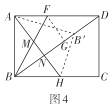
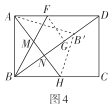
（3）前进小组在创新小组的操作基础上，将图3中的纸片展开，再将矩形纸片沿直线折叠，使得点落在对角线上的点处，然后将纸片展平．如图4所示，折痕交于点，交于点，试判断的形状并证明你的结论．

Answer 1

【答案】（1）证明见解析；（2）；（3）为等腰三角形，理由见解析．

【解析】

（1）利用矩形和折叠的性质分别得到，，，，然后根据AAS定理证明，从而求证；

（2）根据勾股定理求得BD的长，设AF=FG=x，然后利用折叠的性质及勾股定理列方程求出AF的值，最后再利用勾股定理求BF；

（3）利用折叠的性质得到垂直平分，从而得到及，然后利用等角对等边判定三角形的形状．

解：（1）如图2，四边形为矩形，

，，

由折叠得，，

，

在和中，

，

；

（2）如图3，由题意可知：AB=BG=3，AD=4，∠A=∠FGB=90°

∴BD=

∴DG=BD-BG=5-3=2

设AF=FG=x，则DF=4-x

在Rt△FGD中，

解得：

在Rt△ABF中，

故答案为：；

（3）如图4，为等腰三角形．

理由如下：

折叠得到，

垂直平分，

．

又，

，

．

又折叠得到，

，

，

，

为等腰三角形．