题目内容
【题目】如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF、DE、EF与AC交于点O,DE与交于点G,连接OG,若![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③EF⊥AC;④
;③EF⊥AC;④![]() .其中正确的结论的序号是___________.
.其中正确的结论的序号是___________.

【答案】①③④
【解析】
根据等边三角形的性质求出∠EAC=60°,AE=AC,求出BC=AF,根据SAS证△ABC≌△EFA,推出FE=AB,∠AEF=∠BAC=30°,求出∠AOE=90°,即可判断③;求出AD=BD,BF=AF,∠DFB=∠EAF,∠BDF=∠AEF,根据AAS证△DBF≌△EFA,即可判断①;得出四边形ADFE为平行四边形,推出AG=![]() AF,AG=
AF,AG=![]() AB,求出AD=AB,推出AD=4AG,即可判断④;求出∠FAE=90°,∠AFE<90°,推出EF>AE,即可判断②.
AB,求出AD=AB,推出AD=4AG,即可判断④;求出∠FAE=90°,∠AFE<90°,推出EF>AE,即可判断②.
∵△ACE是等边三角形
∴![]()
∵![]()
∴![]()
∵F为AB的中点
∴![]()
∴![]()
在△ABC和△EFA中
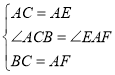
∴![]()
∴![]() ,
,![]()
∴![]() ,故③正确
,故③正确
∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
在△DBF和△EFA中
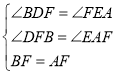
∴![]() ,故①正确
,故①正确
∴![]()
∵![]()
∴四边形ADFE为平行四边形
∴![]()
∵![]()
∴![]() ,故④正确
,故④正确
∵四边形ADFE为平行四边形
∴![]()
∵![]()
∴![]()
∴![]() ,故②错误
,故②错误
正确的有①③④
故答案为:①③④.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】七(一)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):
月均用水量x/m3 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 | x>20 |
频数/户 | 12 | 20 | 3 | ||
频率 | 0.12 | 0.07 |
若该小区有800户家庭,据此估计该小区月均用水量不超过10m3的家庭约有________户.
【题目】某中学举行“中国梦·校园好声音”歌手大赛,高、初中根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩(满分100)如下图所示:

根据图示信息,整理分析数据如下表:
平均数(分) | 中位数(分) | 众数(分) | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
(说明:图中虚线部分的间隔距离均相等)
(1)求出表格中![]() 的值;
的值;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.


