题目内容
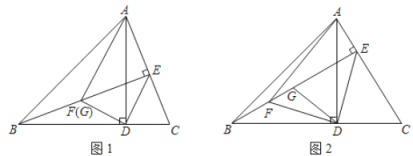
【题目】锐角△ABC 中,BC=6,BC 边上的高 AD=4,两动点 M,N 分别在边 AB,AC 上滑动(M 不与 A、B 重合),且 MN∥BC,以 MN 为边向下作正方形 MPQN,设其边长为 x,正方形 MPQN 与△ABC 公共部分的面积为 y(y>0).
(1)MN,BC具备什么条件,△AMN∽△ABC;
(2)当 x为何值时,PQ 恰好落在边 BC 上(如图 1);
(3)当 PQ 在△ABC 外部时(如图 2),求 y 关于 x 的函数关系式(注明 x 的取值范围)并求出 x 为何值时 y 最大,最大值是多少?

【答案】(1)MN∥BC;(2)x=![]() ;(3)当 x=3 时,y 有最大值,最大值是 6.
;(3)当 x=3 时,y 有最大值,最大值是 6.
【解析】
(1)根据 MN∥BC,得△AMN∽△ABC;(2)因为正方形的位置在变化,但是△AMN∽△ABC 没有改变,利用相似三角形对应边上高的比等于相似比,得出等量关系,代入解析式;(3)用含 x 的式子表示矩形 MEFN 边长,从而求出面积的表达式.
(1)∵MN∥BC,
∴△AMN∽△ABC;
(2)当 PQ 恰好落在边 BC上时,
∵MN∥BC,∴△AMN∽△ABC.
∴![]() ,
,
即 ![]() ,x=
,x= ![]() ;
;
(3)设 BC 分别交 MP,NQ 于 E,F,则四边形 MEFN 为矩形.
设 ME=NF=h,AD 交 MN 于 G(如图 2)GD=NF=h,AG=4﹣h.
∵MN∥BC,
∴△AMN∽△ABC.
∴![]() ,即
,即 ![]() ,
,
∴h=﹣![]() x+4.
x+4.
∴y=MNNF=x(﹣![]() x+4)=-
x+4)=-![]() x+4x(2.4<x<6),
x+4x(2.4<x<6),
配方得:y=﹣![]() (x﹣3)+6.
(x﹣3)+6.
∴当 x=3 时,y 有最大值,最大值是 6.

【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.