题目内容
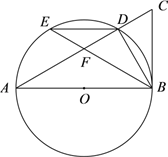
【题目】如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.
(1)求证:BC是⊙O的切线;
(2)当点E为弧AD的中点且∠BED=30°时,⊙O半径为2,求DF的长度.
【答案】(1)证明见解析;(2)![]()
【解析】由圆周角定理和已知条件证出∠CBD+∠ABD=90°.得出∠ABC=90°,即可得出结论;
(2) 在RtΔBDF中,利用三角函数即可求出DF的长度.
解:(1)证明:∵AB为⊙O的直径,
∴∠ADB=90°,∴∠A+∠DBA=90°,
∵ 弧BD=弧BD,∴∠A=∠E,
∵∠CBD=∠E,∴∠CBD=∠A ,
∴∠CBD +∠DBA=90°,∴AB⊥BC,
∴BC是⊙O的切线.
(2)解:∵∠BED=30°,
∴∠A=∠E=∠CBD=30°,
∴∠DBA=60°,
∵点E为弧AD的中点,
∴∠EBD=∠EBA=30°,
∵⊙O半径为2,
∴AB=4,BD=2,AD= ![]() .
.
在RtΔBDF中,∠DBF=90°,
![]() ,
,
∴DF![]() .
.
“点睛”本题考查了切线的判定定理、圆周角定理、三角函数等知识,熟练掌握切线的判定,由三角函数求出直径是解决问题(2)的关键.

练习册系列答案
相关题目