ƒøƒ⁄»ð
°æƒø°ø◊€∫œ”ÎÃΩæø
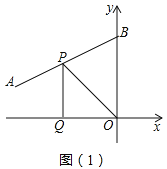
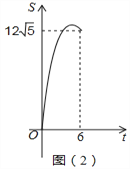
»ÁÕº£®1£©£¨œþ∂ŒABµƒ¡Ω∏ˆ∂Àµ„µƒ◊¯±Í∑÷±Œ™£®-12£¨4£©£®0£¨10£©£¨µ„P¥”µ„B≥ˆ∑¢£¨—ÿBA∑ΩœÚ‘»ÀŸœÚµ„A‘À∂Ø£ªÕ¨ ±£¨µ„Q¥”◊¯±Í‘≠µ„O≥ˆ∑¢£¨—ÿx÷·µƒ∑¥∑ΩœÚ“‘œýÕ¨µƒÀŸ∂»‘À∂Ø£¨µ±µ„PµΩ¥Ôµ„A ±£¨P,Q¡Ωµ„Õ¨ ±Õ£÷π‘À∂Ø£¨…Ë‘À∂صƒ ±º‰Œ™t√Σ¨¶§OPQµƒ√ʪ˝S£®∆Ω∑Ωµ•Œª£©”Î ±º‰t£®√Σ©÷ƺ‰µƒ∫Ø ˝ÕºœÛ»ÁÕº£®2£©À˘ æ°£
£®1£©«Ûµ„Pµƒ‘À∂ØÀŸ∂»£ª
£®2£©«Û√ʪ˝S”Îtµƒ∫Ø ˝πÿœµ Ωº∞µ±S◊Ó◊Ó¥Û÷µ ±µ„Pµƒ◊¯±Í£ª
£®3£©µ„P «S»°◊Ó¥Û÷µ ±µƒµ„£¨…˵„MŒ™x÷·…œµƒµ„£¨µ„NŒ™◊¯±Í∆Ω√ʃ⁄µƒµ„£¨“‘µ„O,P£¨M,NŒ™∂•µ„µƒÀƒ±þ–Œµÿæÿ–Œ£¨«Î÷±Ω”–¥≥ˆµ„Nµƒ◊¯±Í°£
°æ¥∞∏°ø£®1£©µ„Pµƒ‘À∂ØÀŸ∂»Œ™![]() £®≥§∂»µ•Œª°¢√Σ©£ª£®2£©¶§OPQµƒ√ʪ˝S”Ît÷ƺ‰µƒ∫Ø ˝πÿœµ ΩŒ™
£®≥§∂»µ•Œª°¢√Σ©£ª£®2£©¶§OPQµƒ√ʪ˝S”Ît÷ƺ‰µƒ∫Ø ˝πÿœµ ΩŒ™![]() £¨µ„Pµƒ◊¯±ÍŒ™£®-10£¨5£©£ª£®3£©N1(0,5)N2(
£¨µ„Pµƒ◊¯±ÍŒ™£®-10£¨5£©£ª£®3£©N1(0,5)N2(![]() )
)
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫
£®1£©«Û≥ˆABµƒ≥§£¨∏˘æðÀŸ∂»=![]() £¨º∆À„º¥ø…£ª
£¨º∆À„º¥ø…£ª
£®2£©”…Rt°˜ADB°◊Rt°˜PCB£¨ø…µ√![]() £¨ø…µ√PC=2t£¨BC=t£¨Õ∆≥ˆOC=10©Åt£¨Õ∆≥ˆµ„Pµƒ◊¯±ÍŒ™£®©Å2t£¨10©Åt£©£¨OQ=
£¨ø…µ√PC=2t£¨BC=t£¨Õ∆≥ˆOC=10©Åt£¨Õ∆≥ˆµ„Pµƒ◊¯±ÍŒ™£®©Å2t£¨10©Åt£©£¨OQ=![]() t£¨Õ∆≥ˆS=
t£¨Õ∆≥ˆS=![]() OQPE=
OQPE=![]() °¡
°¡![]() t£®10©Åt£©£¨¿˚”√∂˛¥Œ∫Ø ˝µƒ–‘÷ º¥ø…Ω‚æˆŒ £ª
t£®10©Åt£©£¨¿˚”√∂˛¥Œ∫Ø ˝µƒ–‘÷ º¥ø…Ω‚æˆŒ £ª
£®3£©∑÷¡Ω÷÷«È–ŒÃ÷¬€«ÛΩ‚£ª
‘Ã‚Ω‚Œˆ£∫
£®1£©◊˜PC°ÕOB”⁄C£¨AD°ÕOB”⁄D£¨PE°ÕOQ”⁄E£Æ
°þA£®©Å12£¨4£©£¨B£®0£¨10£©£¨
°ýAD=12£¨OD=4£¨0B=10£¨
°ýBD=6£¨
‘⁄Rt°˜ADB÷–£¨AB=![]() £¨
£¨
”…ÕºœÛø…÷™£¨µ„P‘À∂Ø ±º‰Œ™6√Σ¨
°ýµ„Pµƒ‘À∂ØÀŸ∂»Œ™6![]() °¬6=
°¬6=![]() £®≥§∂»µ•Œª/√Σ©£Æ
£®≥§∂»µ•Œª/√Σ©£Æ
£®2£©…˵„P‘À∂Ø¡Àt√Σ¨‘ÚBP=OQ=![]() t£¨
t£¨
°þ°œPBC=°œABD£¨°œADB=°œPCB=90°„£¨
°ýRt°˜ADB°◊Rt°˜PCB£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
°ýPC=2t£¨BC=t£¨
°ýOC=10©Åt£¨
°ýµ„Pµƒ◊¯±ÍŒ™£®©Å2t£¨10©Åt£©£¨OQ=![]() t£¨
t£¨
°ýS=![]() OQPE=
OQPE=![]() °¡
°¡![]() t£®10©Åt£©£¨
t£®10©Åt£©£¨
°ýS=©Å![]() t2+5
t2+5![]() t=©Å
t=©Å![]() £®t©Å5£©2+
£®t©Å5£©2+![]() £®0°Ðt°Ð6£©£¨
£®0°Ðt°Ð6£©£¨
°þ©Å![]() £º0£¨
£º0£¨
°ýµ±t=5 ±£¨S»°µ√◊Ó¥Û÷µ£¨
¥À ±©Å2t=©Å10£¨10©Åt=10©Å5=5£¨º¥µ„Pµƒ◊¯±ÍŒ™£®©Å10£¨5£©£¨
◊€…œÀ˘ ˆ£¨°˜OPQµƒ√ʪ˝S”Îtµƒ∫Ø ˝πÿœµ ΩŒ™S=©Å![]() t2+5
t2+5![]() t£®0°Ðt°Ð6£©£¨
t£®0°Ðt°Ð6£©£¨
µ±√ʪ˝◊Ó¥Û ±£¨µ„Pµƒ◊¯±ÍŒ™£®©Å10£¨5£©£Æ
£®3£©»ÁÕº£¨

¢Ÿµ±PM1°Õx÷·£¨PN1°Õy÷· ±£¨Àƒ±þ–ŒPM1ON1 «æÿ–Œ£¨¥À ±N1£®0£¨5£©£Æ
¢⁄µ±PM2°ÕOP ±£¨ø…µ√Àƒ±þ–ŒPM2N2O «æÿ–Œ£¨
°þ÷±œþOPµƒΩ‚Œˆ ΩŒ™y=©Å![]() x£¨
x£¨
°ý÷±œþPM2µƒΩ‚Œˆ ΩŒ™y=2x+25£¨ø…µ√M2£®©Å12.5£¨0£©£¨…ËN2£®m£¨n£©£¨
‘Ú”–![]() £¨
£¨
°ým=©Å![]() £¨n=©Å5£¨
£¨n=©Å5£¨
°ýN2£®©Å![]() £¨©Å5£©£¨
£¨©Å5£©£¨
◊€…œÀ˘ ˆ£¨¬˙◊„Ãıº˛ «µ„N1£®0£¨5£©£¨N2£®©Å![]() £¨©Å5£©£Æ
£¨©Å5£©£Æ

 √˚ÂΩæÌœµ¡–¥∞∏
√˚ÂΩæÌœµ¡–¥∞∏