题目内容
【题目】王达和李力是八(2)班运动素质最好的两位同学,为了选出一名同学参加全校的体育运动大寒,班主任针对学校要测试的五个项目,对两位同学进行相应的测试(成绩:分),结果如下:
姓名 | 力量 | 速度 | 耐力 | 柔韧 | 灵敏 |
王达 | 60 | 75 | 100 | 90 | 75 |
李力 | 70 | 90 | 80 | 80 | 80 |
根据以上测试结果解答下列问题:
(1)补充完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差(分2) |
王达 | 80 | 75 | 75 | 190 |
李力 |
(2)任选一个角度分析推选哪位同学参加学校的比赛比较合适?并说明理由;
(3)若按力量:速度:耐力:柔韧:灵敏=1:2:3:3:1的比例折合成综合分数,推选得分同学参加比赛,请通过计算说明应推选哪位同学去参赛。
【答案】(1)80,80,80,40 (2)答案见解析 (3)李力
【解析】
(1)利用平均数的计算方法求出李力测试成绩的平均数,再求出中位数和众数,然后利用方差公式求出李力测试成绩的方差,填表即可;
(2)可以根据表中数据,从两人的平均数,中位数,众数,方差进行分析,可得出结果;
(3)根据已知力量:速度:耐力:柔韧:灵敏=1:2:3:3:1的比例折合成综合分数,分别算出两人的综合分数,再比较大小即可得出去参加比赛的选手.
(1)解:李力的平均成绩为:![]() ;
;
将5个数排序70,80,80,80,90,
最中间的数是80,
∴李力的测试成绩的中位数为80;
∵80出现了3次,是这组数据中出现次数最多的数,
∴这组数据的众数是80;
李力测试成绩的方差为:![]() ,
,
填表如下
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差(分2) |
王达 | 80 | 75 | 75 | 190 |
李力 | 80 | 80 | 80 | 40 |
(2)解:根据表中数据可知,两人的平均成绩相同,从中位数和众数看,李力的成绩比王达的成绩好,从方差看,李力测试成绩的方差比王达次数成绩的方差小,可知李力的成绩比王达的成绩稳定,因此应该推选李力参加比赛。
(3)解:∵按力量:速度:耐力:柔韧:灵敏=1:2:3:3:1的比例折合成综合分数,
∴王达的成绩为:60×1+75×2+100×3+90×3+75×1=855;
李力的成绩为:70×1+90×2+80×3+80×3+80×1=910;
910>855
∴选李力去参加比赛.

【题目】我乡某校举行全体学生“定点投篮”比赛,每位学生投40个,随机抽取了部分学生的投篮结果,并绘制成如下统计图表。
组别 | 投进个数 | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 30 |
D |
| m |
E |
| n |
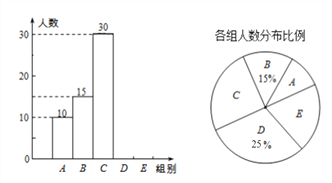
根据以上信息完成下列问题。
①本次抽取的学生人数为多少?
②统计表中的m=__________;
③扇形统计图中E组所占的百分比;
④补全频数分布直方图;
⑤扇形统计图中“C组”所对应的圆心角的度数;
⑥本次比赛中投篮个数的中位数落在哪一组;
⑦已知该校共有900名学生,如投进个数少于24个定为不合格,请你估计该校本次投篮比赛不合格的学生人数.