Question

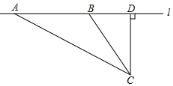
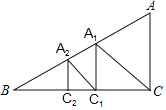
【题目】如图，已知直角△ABC中，AC＝6，BC＝8，过直角顶点C作CA1⊥AB，垂足为A1，再过A作A1C1⊥BC，垂足为C1，过C1作C1A2⊥AB，垂足为A2，再过A2作A2C2⊥BC，垂足为C2，……，则＝_____（其中n为正整数）．

Answer 1

【答案】

【解析】

利用勾股定理可求出AB的长，然后由CA1⊥AB，得出△A1CA∽△CBA，利用相似三角形的性质求出CA1＝，，同理根据相似三角形的性质可求出△nAnCn﹣1∽△CBA，继而得出答案．

解：在Rt△ABC中，AC=6，BC=8，

由勾股定理得AB，

∵CA1⊥AB，∠ACB＝90°，

∴△A1CA∽△CBA，

∴，

解得，CA1=，

∵A1C1∥AC，

∴∠ACA1=∠CA1C1，

∴△A1C1C∽△CA1A，

∴

由平行线的性质，得∠A1CA=∠nAnCn﹣1，

∴△nAnCn﹣1∽△CBA，

∴．

故答案为：．