题目内容
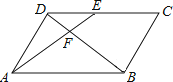
【题目】如图，△ABC中，E、D分别是AC、BC的中点，AD、BE交于点O ， 则S△DOE：S△AOB=（ ） 
A.1：2
B.2：3
C.1：3
D.1：4
【答案】D
【解析】解答：∵△ABC中，E、D分别是AC、BC的中点，∴DE= 
AB ， DE∥AB ，
∴△DOE∽△AOB ，
∴S△DOE：S△AOB=1：4．
故选：D ．
分析：根据三角形中位线定理可得DE= AB ， DE∥AB ， 再根据平行线性质和相似三角形的判定与性质即可求解．
【考点精析】掌握相似三角形的判定与性质是解答本题的根本，需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
