Ő‚ńŅńŕ»›
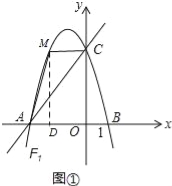
°ĺŐ‚ńŅ°Ņ»ÁÕľĘŔ£¨÷ĪŌŖy=![]() x+4ĹĽ”ŕx÷Š”ŕĶ„A£¨ĹĽy÷Š”ŕĶ„C£¨ĻżA°ĘCŃĹĶ„ĶńŇ◊őÔŌŖF1ĹĽx÷Š”ŕŃŪ“ĽĶ„B£®1£¨0£©£ģ
x+4ĹĽ”ŕx÷Š”ŕĶ„A£¨ĹĽy÷Š”ŕĶ„C£¨ĻżA°ĘCŃĹĶ„ĶńŇ◊őÔŌŖF1ĹĽx÷Š”ŕŃŪ“ĽĶ„B£®1£¨0£©£ģ
£®1£©«ůŇ◊őÔŌŖF1ňýĪŪ ĺĶń∂ĢīőļĮ żĶńĪŪīÔ Ĺ£Ľ
£®2£©»ŰĶ„M «Ň◊őÔŌŖF1őĽ”ŕĶŕ∂ĢŌůŌřÕľŌů…ŌĶń“ĽĶ„£¨…ŤňńĪŖ–őMAOCļÕ°ųBOCĶń√śĽż∑÷Īūő™SňńĪŖ–őMAOCļÕS°ųBOC£¨ľ«S=SňńĪŖ–őMAOC©ĀS°ųBOC£¨«ůS◊Óīů ĪĶ„MĶń◊ÝĪÍľįSĶń◊Óīů÷Ķ£Ľ
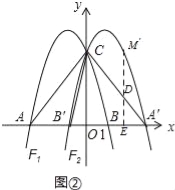
£®3£©»ÁÕľĘŕ£¨ĹęŇ◊őÔŌŖF1—ōy÷Š∑≠’Ř≤Ę°įłī÷∆°ĪĶ√ĶĹŇ◊őÔŌŖF2£¨Ķ„A°ĘB”Ž£®2£©÷–ňý«ůĶńĶ„MĶń∂‘”¶Ķ„∑÷Īūő™A°š°ĘB°š°ĘM°š£¨ĻżĶ„M°š◊ųM°šE°Õx÷Š”ŕĶ„E£¨ĹĽ÷ĪŌŖA°šC”ŕĶ„D£¨‘ŕx÷Š…Ō «∑Ůīś‘ŕĶ„P£¨ ĻĶ√“‘A°š°ĘD°ĘPő™∂•Ķ„Ķń»żĹ«–ő”Ž°ųAB°šCŌŗň∆£Ņ»Űīś‘ŕ£¨«Ž«ů≥ŲĶ„PĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ£®1£©y=©Ā![]() x2©Ā
x2©Ā![]() x+4£Ľ£®2£©◊Óīů÷Ķő™
x+4£Ľ£®2£©◊Óīů÷Ķő™![]() £ĽM£®©Ā
£ĽM£®©Ā![]() £¨5£©£Ľ£®3£©£®2£¨0£©ĽÚ£®©Ā
£¨5£©£Ľ£®3£©£®2£¨0£©ĽÚ£®©Ā![]() £¨0£©
£¨0£©
°ĺĹ‚őŲ°Ņ
‘Ő‚∑÷őŲ£ļ£®1£©ņŻ”√“ĽīőļĮ żĶńĹ‚őŲ Ĺ«ů≥ŲĶ„A°ĘCĶń◊ÝĪÍ£¨»Ľļů‘ŔņŻ”√BĶ„◊ÝĪÍľīŅ…«ů≥Ų∂ĢīőļĮ żĶńĹ‚őŲ Ĺ£Ľ£®2£©”…”ŕM‘ŕŇ◊őÔŌŖF1…Ō£¨ňý“‘Ņ……ŤM£®a£¨©Ā![]() a2©Ā
a2©Ā![]() a+4£©£¨»Ľļů∑÷Īūľ∆ň„SňńĪŖ–őMAOCļÕS°ųBOC£¨ĻżĶ„M◊ųMD°Õx÷Š”ŕĶ„D£¨‘ÚSňńĪŖ–őMAOCĶń÷ĶĶ»”ŕ°ųADMĶń√śĽż”ŽŐ›–őDOCMĶń√śĽż÷ģļÕ£Ľ£®3£©”…”ŕ√Ľ”–ňĶ√ųĶ„PĶńĺŖŐŚőĽ÷√£¨ňý“‘–Ť“™ĹęĶ„PĶńőĽ÷√ĹÝ––∑÷ņŗŐ÷¬Ř£¨ĶĪĶ„P‘ŕA°šĶń”“ĪŖ Ī£¨īň«ťŅŲ «≤Ľīś‘ŕ£ĽĶĪĶ„P‘ŕA°šĶń◊ůĪŖ Ī£¨īň Ī°ŌDA°šP=°ŌCAB°š£¨»Ű“‘A°š°ĘD°ĘPő™∂•Ķ„Ķń»żĹ«–ő”Ž°ųAB°šCŌŗň∆£¨‘Ú∑÷ő™“‘Ō¬ŃĹ÷÷«ťŅŲĹÝ––Ő÷¬Ř£ļĘŔ
a+4£©£¨»Ľļů∑÷Īūľ∆ň„SňńĪŖ–őMAOCļÕS°ųBOC£¨ĻżĶ„M◊ųMD°Õx÷Š”ŕĶ„D£¨‘ÚSňńĪŖ–őMAOCĶń÷ĶĶ»”ŕ°ųADMĶń√śĽż”ŽŐ›–őDOCMĶń√śĽż÷ģļÕ£Ľ£®3£©”…”ŕ√Ľ”–ňĶ√ųĶ„PĶńĺŖŐŚőĽ÷√£¨ňý“‘–Ť“™ĹęĶ„PĶńőĽ÷√ĹÝ––∑÷ņŗŐ÷¬Ř£¨ĶĪĶ„P‘ŕA°šĶń”“ĪŖ Ī£¨īň«ťŅŲ «≤Ľīś‘ŕ£ĽĶĪĶ„P‘ŕA°šĶń◊ůĪŖ Ī£¨īň Ī°ŌDA°šP=°ŌCAB°š£¨»Ű“‘A°š°ĘD°ĘPő™∂•Ķ„Ķń»żĹ«–ő”Ž°ųAB°šCŌŗň∆£¨‘Ú∑÷ő™“‘Ō¬ŃĹ÷÷«ťŅŲĹÝ––Ő÷¬Ř£ļĘŔ![]() =
=![]() £ĽĘŕ
£ĽĘŕ![]() =
=![]() £ģ
£ģ
‘Ő‚Ĺ‚őŲ£ļĹ‚£ļ£®1£©ŃÓy=0īķ»Žy=![]() x+4£¨
x+4£¨
°ŗx=©Ā3£¨
A£®©Ā3£¨0£©£¨
ŃÓx=0£¨īķ»Žy=![]() x+4£¨
x+4£¨
°ŗy=4£¨
°ŗC£®0£¨4£©£¨
…ŤŇ◊őÔŌŖF1ĶńĹ‚őŲ Ĺő™£ļy=a£®x+3£©£®x©Ā1£©£¨
į—C£®0£¨4£©īķ»Ž…Ō ĹĶ√£¨a=©Ā![]() £¨
£¨
°ŗy=©Ā![]() x2©Ā
x2©Ā![]() x+4£¨
x+4£¨
£®2£©»ÁÕľĘŔ£¨…ŤĶ„M£®a£¨©Ā![]() a2©Ā
a2©Ā![]() a+4£©
a+4£©
∆š÷–©Ā3£ľa£ľ0
°ŖB£®1£¨0£©£¨C£®0£¨4£©£¨
°ŗOB=1£¨OC=4
°ŗS°ųBOC=![]() OBOC=2£¨
OBOC=2£¨
ĻżĶ„M◊ųMP°Õx÷Š”ŕĶ„P£¨
°ŗMP=©Ā![]() a2©Ā
a2©Ā![]() a+4£¨AP=a+3£¨OP=©Āa£¨
a+4£¨AP=a+3£¨OP=©Āa£¨
°ŗSňńĪŖ–őMAOC=![]() APMP+
APMP+![]() £®MP+OC£©OP
£®MP+OC£©OP
=![]() APMP+
APMP+![]() OPMP+
OPMP+![]() OPOC
OPOC
=![]() +
+![]()
=![]() +
+![]()
=![]() °Ń3£®©Ā
°Ń3£®©Ā![]() a2©Ā
a2©Ā![]() a+4£©+
a+4£©+![]() °Ń4°Ń£®©Āa£©
°Ń4°Ń£®©Āa£©
=©Ā2a2©Ā6a+6
°ŗS=SňńĪŖ–őMAOC©ĀS°ųBOC
=£®©Ā2a2©Ā6a+6£©©Ā2
=©Ā2a2©Ā6a+4
=©Ā2£®a+![]() £©2+
£©2+![]()
°ŗĶĪa=©Ā![]() Ī£¨
Ī£¨
S”–◊Óīů÷Ķ£¨◊Óīů÷Ķő™![]()
īň Ī£¨M£®©Ā![]() £¨5£©£Ľ
£¨5£©£Ľ
£®3£©»ÁÕľĘŕ£¨”…Ő‚“‚÷™£ļM°š£®![]() £©£¨
£©£¨
°ŗAB°š=2£¨
…Ť÷ĪŌŖA°šCĶńĹ‚őŲ Ĺő™£ļy=kx+b£¨
į—A°š£®3£¨0£©ļÕC£®0£¨4£©īķ»Žy=kx+b£¨
Ķ√£ļ![]() £¨
£¨
°ŗ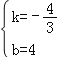
°ŗy=©Ā![]() x+4£¨
x+4£¨
ŃÓx=![]() īķ»Žy=©Ā
īķ»Žy=©Ā![]() x+4£¨
x+4£¨
°ŗy=2
°ŗ![]()
”…ĻīĻ…∂®ņŪ∑÷ĪūŅ…«ůĶ√£ļAC=5£¨DA°š=![]()
…ŤP£®m£¨0£©
ĶĪm£ľ3 Ī£¨
īň ĪĶ„P‘ŕA°šĶń◊ůĪŖ£¨
°ŗ°ŌDA°šP=°ŌCAB°š£¨
ĶĪ![]() =
=![]() Ī£¨°ųDA°šP°◊°ųCAB°š£¨
Ī£¨°ųDA°šP°◊°ųCAB°š£¨
īň Ī£¨![]() =
=![]() £®3©Ām£©£¨
£®3©Ām£©£¨
Ĺ‚Ķ√£ļm=2£¨
°ŗP£®2£¨0£©
ĶĪ![]() =
=![]() Ī£¨°ųDA°šP°◊°ųB°šAC£¨
Ī£¨°ųDA°šP°◊°ųB°šAC£¨
īň Ī£¨![]() =
=![]() £®3©Ām£©
£®3©Ām£©
m=©Ā![]() £¨
£¨
°ŗP£®©Ā![]() £¨0£©
£¨0£©
ĶĪm£ĺ3 Ī£¨
īň Ī£¨Ķ„P‘ŕA°š”“ĪŖ£¨
”…”ŕ°ŌCB°šO°Ŕ°ŌDA°šE£¨
°ŗ°ŌAB°šC°Ŕ°ŌDA°šP
°ŗīň«ťŅŲ£¨°ųDA°šP”Ž°ųB°šAC≤Ľń‹Ōŗň∆£¨
◊Ř…Ōňý Ų£¨ĶĪ“‘A°š°ĘD°ĘPő™∂•Ķ„Ķń»żĹ«–ő”Ž°ųAB°šCŌŗň∆ Ī£¨Ķ„PĶń◊ÝĪÍő™£®2£¨0£©ĽÚ£®©Ā![]() £¨0£©£ģ
£¨0£©£ģ