题目内容
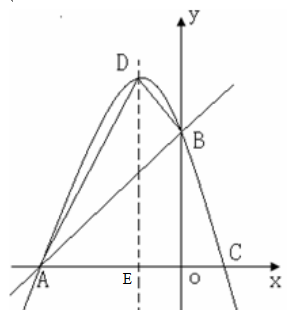
如图,直线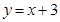 交x轴于A点,交y轴于B点,抛物线
交x轴于A点,交y轴于B点,抛物线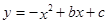 经过点A、B,交x轴于另一点C,顶点为D.
经过点A、B,交x轴于另一点C,顶点为D.
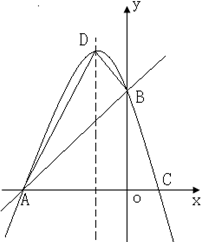
(1)求抛物线的函数表达式;
(2)求点C、D两点的坐标;
(3)求△ABD的面积;
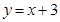 交x轴于A点,交y轴于B点,抛物线
交x轴于A点,交y轴于B点,抛物线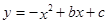 经过点A、B,交x轴于另一点C,顶点为D.
经过点A、B,交x轴于另一点C,顶点为D.
(1)求抛物线的函数表达式;
(2)求点C、D两点的坐标;
(3)求△ABD的面积;
(1)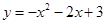 ;(2)c(1,0),D(-1,4);(3)3.
;(2)c(1,0),D(-1,4);(3)3.
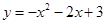 ;(2)c(1,0),D(-1,4);(3)3.
;(2)c(1,0),D(-1,4);(3)3.试题分析:(1)求出A、B的坐标,代入抛物线的解析式即可;
(2)令
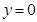 ,即可求出抛物线与
,即可求出抛物线与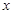 轴的两个交点,把抛物线化成顶点式即可得到顶点坐标;
轴的两个交点,把抛物线化成顶点式即可得到顶点坐标;(3)设对称轴与x轴交于点E,则△ABD的面积=△ADE的面积+梯形DEOB的面积-△AOB的面积.
试题解析:(1)在
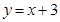 中,令
中,令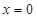 ,得
,得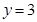 ,∴B(0,3);令
,∴B(0,3);令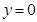 ,得:
,得: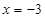 ,∴A(-3,0),∴
,∴A(-3,0),∴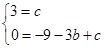 ,解得:
,解得: ,∴抛物线的解析式为:
,∴抛物线的解析式为: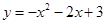 ;
;(2)在
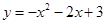 中,令
中,令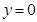 ,得:
,得: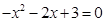 ,解得:
,解得: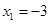 ,
,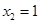 ,∴C(1,0),∵
,∴C(1,0),∵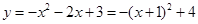 ∴顶点D的坐标为(-1,4);
∴顶点D的坐标为(-1,4);(3)设抛物线对称轴与
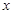 轴相交于点E,∵A(-3,0),B(0,3),D (-1,4),∴AE=2,DE=4,OE=1,OB=3,
轴相交于点E,∵A(-3,0),B(0,3),D (-1,4),∴AE=2,DE=4,OE=1,OB=3,∴

=
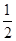 ×AE×DE+
×AE×DE+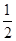 ×(DE+OB) ×OE-
×(DE+OB) ×OE-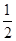 AO×OB=
AO×OB=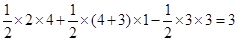 .
.

练习册系列答案
相关题目
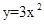 先向左平移1个单位,再向上平移2个单位,那么所得的新抛物线的解析式是( )
先向左平移1个单位,再向上平移2个单位,那么所得的新抛物线的解析式是( )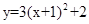
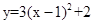
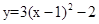
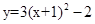
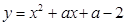
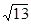 时,求出此二次函数的解析式.
时,求出此二次函数的解析式.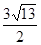 ,若存在求出P点坐标,若不存在请说明理由。
,若存在求出P点坐标,若不存在请说明理由。 的部分图像如图所示,若关于x的一元二次方程
的部分图像如图所示,若关于x的一元二次方程 的一个解为
的一个解为 ,则另一个解
,则另一个解 = .
= .
 中,当x>0时,y随x的增大而增大,则二次函数
中,当x>0时,y随x的增大而增大,则二次函数 的图象大致是图中的( )
的图象大致是图中的( )




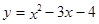 ,当
,当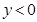 时,自变量
时,自变量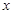 的取值范围是 ;
的取值范围是 ;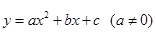 向下平移3个单位,再向左平移4个单位得到抛物线
向下平移3个单位,再向左平移4个单位得到抛物线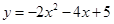 ,则原抛物线的顶点坐标是
,则原抛物线的顶点坐标是