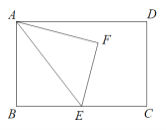
题目内容
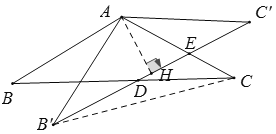
【题目】如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到![]() ,
,![]() 与BC,AC分别交于点D,E.设
与BC,AC分别交于点D,E.设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数图象大致为( )
的函数图象大致为( )
A.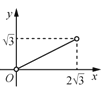 B.
B.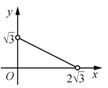 C.
C.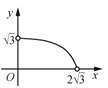 D.
D.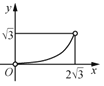
【答案】B
【解析】
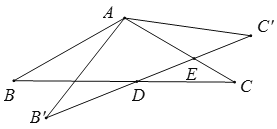
连接B′C,作AH⊥B′C′,垂足为H,由已知以及旋转的性质可得AB′=AB=AC=AC′=2,∠AB′C′=∠C′=30°,继而可求出AH长,B′C′的长,由等腰三角形的性质可得∠AB′C=∠ACB′,再根据∠AB′D=∠ACD=30°,可得∠DB′C=∠DCB′,从而可得B′D=CD,进而可得 B′E=x,由此可得C′E=2![]() -x,再根据三角形面积公式即可求得y与x的关系式,由此即可得到答案.
-x,再根据三角形面积公式即可求得y与x的关系式,由此即可得到答案.
连接B′C,作AH⊥B′C′,垂足为H,
∵AB=AC,∠B=30°,
∴∠C=∠B=30°,
∵△ABC绕点A逆时针旋转α(0<α<120°)得到![]() ,
,
∴AB′=AB=AC=AC′=2,∠AB′C′=∠C′=30°,
∴AH=![]() AC′=1,
AC′=1,
∴C′H=![]() ,
,
∴B′C′=2C′H=2![]() ,
,
∵AB′=AC,
∴∠AB′C=∠ACB′,
∵∠AB′D=∠ACD=30°,
∴∠AB′C-∠AB′D=∠ACB′-∠ACD,
即∠DB′C=∠DCB′,
∴B′D=CD,
∵CD+DE=x,
∴B′D+DE=x,即B′E=x,
∴C′E=B′C′-B′E=2![]() -x,
-x,
∴y=![]() =
=![]() ×(2
×(2![]() -x)×1=
-x)×1=![]() ,
,
观察只有B选项的图象符合题意,
故选B.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目