Question

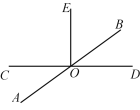
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起（其中，，；）．

（1）①若，则的度数为_____________；

②若，则的度数为_____________．

（2）由（1）猜想与的数量关系，并说明理由．

（3）当且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请写出角度所有可能的值（不必说明理由）；若不存在，请说明理由．

Answer 1

【答案】（1）①；②；（2），理由详见解析；（3）∠ACE=45°或30°或120°或135°或165°

【解析】

（1）①先求出∠ACE，即可求出∠ACB；

②先求出∠ACE，即可求出∠DCE；

（2）根据题意可得，，从而求出与的数量关系；

（3）根据平行线的判定定理和边的平行关系分类讨论，然后画出对应的图形即可得出结论．

解：（1）①∵，∠ACD=∠BCE=90°

∴∠ACE=∠ACD－∠DCE=45°

∴∠ACB=∠ACE＋∠BCE=135°

故答案为：．

②∵，∠ACD=∠BCE=90°

∴∠ACE=∠ACB－∠BCE=50°

∴∠DCE=∠ACD－∠ACE =40°

故答案为：．

（2）．理由如下

∵，，

∴．

∵，，

∴

∴．

（3）①当时，

∵

∴

∴，

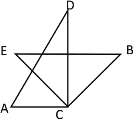
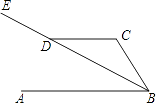
②当时，设CE与AD交于点F，如下图所示

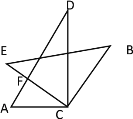
∵∠A=60°，∠BCE=90°

∴∠AFC=180°－∠ACE－∠A=90°

∴∠AFC=∠BCE

∴．

③当时，如下图所示

∵∠ACD=90°，∠D=30°

∴∠DCE=∠ACE－∠ACD=30°

∴∠DCE=∠D

∴．

④当时，如下图所示

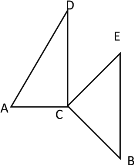
∵∠ACD=90°，∠E=45°

∴∠DCE=∠ACE－∠ACD=45°

∴∠DCE=∠E

∴．

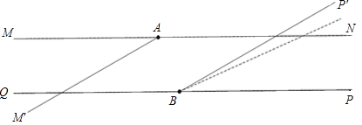
⑤当时，过点C作CG∥AD，如下图所示

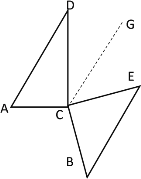
∴∠D=∠DCG=30°

∵∠ACD=90°，∠E=45°

∴∠GCE=∠ACE－∠ACD－∠DCG=45°

∴∠E=∠GCE

∴BE∥CG

∴．

综上所述：∠ACE=45°或30°或120°或135°或165°．