��Ŀ����
����Ŀ�����Ķ����²���.
��ͼ����֪������ABCD�ĶԽ���AC��BD�ڵ�O��E��AC��һ�㣬AG��BE������ΪG.��֤��OE=OF.
֤�������ı���ABCD��������.
���BOE=��AOF=90��,��OA=OE.
�֡�AG��BE�����1+��3��90������2+��3������1����2.
��Rt��BOE��Rt��AOF,��OE=OF.

�Ÿ���������⣬����֤��˼·�ĺ��������� ʹ������Խ������֤�������еĹؼ���֤�� .
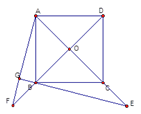
�������������Ϊ����E��AC���ӳ����ϣ�AG��BE��EB���ӳ����ڵ�G���ӳ�AG��DB���ӳ����ڵ�F����ͼ��������������.
��֤��OF=OE.
���𰸡���������ȫ�ȣ���1����2����2����������
�������������������1�����������εĶԽ�������ҡ����ഹֱƽ��֤������1=��2���ٸ���AAS֤����Rt��BOE��Rt��AOF������ȫ����ȫ�ȵ����ʼ���֤��OE=OF��
��2�����������ε��ı���ȣ�ÿ���Խ���ƽ��һ��Խǣ�֤������ABF=��BCE���Ӷ�֤������ABF�ա�BCE������ȫ����ȫ�ȵ����ʼ���֤��OE=OF.
�����������1������֤��˼·�ĺ���������ȫ�������ε�����ʹ������Խ������֤�������еĹؼ���֤����1=��2��
�ʴ�Ϊ��ȫ�������ε�����ʹ������Խ������1=��2.
��2����ABCD����������
���ABO=��ACB=45�� ��AB=BC�� OB=OC��
���ABF=��BCE=135�� ��
�ߡ�OAF+��F=90�� ����OAF+��E=90����
���ABF�ա�BCE(AAS)
��BF=CE��
��BF+OB=CE+OC����OE=OF.

 ��У����ϵ�д�
��У����ϵ�д�