题目内容
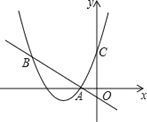
【题目】在平面直角坐标系xOy中，抛物线y=ax2+bx+c的开口向上，且经过点A(0, 
).
（1）若此抛物线经过点B（2，-
），且与
轴相交于点E、F.
①填空：b= （用含a的代数式表示）；
②当EF的值最小时，求出EF的最小值和抛物线的解析式；
（2）若
，当
，抛物线上的点到x轴距离的最大值为3时，求b的值.
【答案】（1）①b=-2a-1；②EF有最小值
，抛物线解析式为y=x2﹣3x+
；（2）b的值为1或﹣5．
【解析】试题分析：（1）①由A点坐标可求得c，再把B点坐标代入可求得b与a的关系式，可求得答案；②用a可表示出抛物线解析式，令y=0可得到关于x的一元二次方程，利用根与系数的关系可用a表示出EF的值，再利用函数性质可求得其取得最小值时a的值，可求得抛物线解析式；
（2）可用b表示出抛物线解析式，可求得其对称轴为x=-b，由题意可得出当x=0、x=1或x=-b时，抛物线上的点可能离x轴最远，可分别求得其函数值，得到关于b的方程，可求得b的值．
试题解析：（1）①∵抛物线y=ax2+bx+c的开口向上，且经过点A（0， 
），
∴c=
，
∵抛物线经过点B（2，-
），
∴-
=4a+2b+
，
∴b=-2a-1，
故答案为：-2a-1；
②由①可得抛物线解析式为y=ax2-（2a+1）x+
，
令y=0可得ax2-（2a+1）x+
=0，
∵△=（2a+1）2-4a×
=4a2-2a+1=4（a-
）2+
＞0，
∴方程有两个不相等的实数根，设为x1、x2，
∴x1+x2=
，x1x2=
，
∴EF2=（x1-x2）2=（x1+x2）2-4x1x2=
=（
-1）2+3，
∴当a=1时，EF2有最小值，即EF有最小值，
∴抛物线解析式为y=x2-3x+
；
（2）当a=
时，抛物线解析式为y=
x2+bx+
，
∴抛物线对称轴为x=-b，
∴只有当x=0、x=1或x=-b时，抛物线上的点才有可能离x轴最远，
当x=0时，y=
，当x=1时，y=
+b+
=2+b，当x=-b时，y=
（-b）2+b（-b）+
=-
b2+
，
①当|2+b|=3时，b=1或b=-5，且顶点不在范围内，满足条件；
②当|-
b2+
|=3时，b=±3，对称轴为直线x=±3，不在范围内，故不符合题意，
综上可知b的值为1或-5．
