��Ŀ����
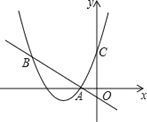
����Ŀ���ס���������ͬʱ��ʼ�ӹ�һ����װ���ӿ�ʼ�ӹ����ӹ���������װ�׳��乤����9Сʱ���ҳ�������;ͣ��һ��ʱ��ά���豸��Ȼ��ͣ��ǰ�Ĺ���Ч�ʼ����ӹ���ֱ����׳���ͬʱ���������װ�ļӹ�����Ϊֹ����ס�����������Լӹ���װ������Ϊy���������׳���ӹ���ʱ��Ϊx��ʱ����y��x֮��ĺ���ͼ����ͼ��ʾ��
��1���׳���ÿСʱ�ӹ���װ����Ϊ�� ������������װ���ܼ���Ϊ�� ������
��2�����ҳ���ά���豸���ҳ���ӹ���װ����y��x֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��3����ס��������乲ͬ�ӹ���1000����װʱ�׳������õ�ʱ�䣮

���𰸡���1��80��1140����2��y=60x��120��4��x��9������3���ס��������乲ͬ�ӹ���1000����װʱ�׳������õ�ʱ��Ϊ8Сʱ��
�������������������1�����ݹ���Ч��=��������¹���ʱ�䣬��������׳���ÿСʱ�ӹ���װ�������ٸ���������װ���ܼ���=�׳����ʽ�ļ���+�ҳ���ӹ��ļ��������ɵ�������װ���ܼ�����
��2�����ݹ���Ч��=���������¹���ʱ�䣬��������ҳ���ÿС���ӹ���װ���������ݹ���ʱ��=���������¹���Ч�ʣ���Ϲ�������ʱ�伴������ҳ������豸��ʱ�䣬�ٸ��ݼӹ��ķ�װ�ܼ���=120+����Ч�ʡ�����ʱ�䣬��������ҳ���ά���豸���ҳ���ӹ���װ����y��x֮��ĺ�����ϵʽ��
��3�����ݼӹ��ķ�װ�ܼ���=����Ч�ʡ�����ʱ�䣬����׳���ӹ���װ����y��x֮��ĺ�����ϵʽ�����ס�������ϵʽ��ӣ��������1000�����ɵý�.
�����������1���׳���ÿСʱ�ӹ���װ����Ϊ720��9=80��������
������װ���ܼ���Ϊ720+420=1140��������
�ʴ�Ϊ��80��1140��
��2���ҳ���ÿСʱ�ӹ���װ����Ϊ120��2=60���������ҳ������豸��ʱ��Ϊ9����420��120����60=4��ʱ����
���ҳ���ά���豸���ҳ���ӹ���װ����y��x֮��ĺ�����ϵʽΪ
y=120+60��x��4��=60x��120��4��x��9����
��3���׳���ӹ���װ����y��x֮��ĺ�����ϵʽΪy=80x��
��80x+60x��120=1000ʱ�� x=8��
�𣺼ס��������乲ͬ�ӹ���1000����װʱ�׳������õ�ʱ��Ϊ8Сʱ��

����Ŀ��ѧУ����Ȥζ�˶��Ὺ���ˡ��������֡���Ŀ����(5)��ס�������С�鶼������༶������Ϊ��ѡ��һ���ȽϺõĶ��飬��(5)��İ�ί��֯��һ��ѡ�������ס��������10�˵ı����ɼ����±���
���� | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
���� | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)����ɼ�����λ���� �֣�����ɼ��������� ����
(2)���������ƽ���ɼ��ͷ�����
(3)��֪����ɼ��ķ�����1.4����ѡ�� �������(5)��μ�ѧУ������