Question

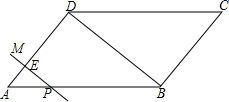
如图，在平行四边形ABCD中，AD=4cm，∠A=60°，BD⊥AD．一动点P从A出发，以每秒1cm的速度沿A→B→C的路线匀速运动，过点P作直线PM，使PM⊥AD．
（1）当点P运动2秒时，设直线PM与AD相交于点E，求△APE的面积；
（2）当点P运动2秒时，另一动点Q也从A出发沿A→B→C的路线运动，且在AB上以每秒1cm的速度匀速运动，在BC上以每秒2cm的速度匀速运动．过Q作直线QN，使QN∥PM．设点Q运动的时间为t秒（0≤t≤10），直线PM与QN截平行四边形ABCD所得图形的面积为Scm²．
①求S关于t的函数关系式；
②（附加题）求S的最大值．

Answer 1

分析：（1）在三角形AEP中，AP=2，∠A=60°，利用三角函数可求出AE和PE，即可求出面积；
（2）①此题应分情况讨论，因为两个动点运动速度不同，所以有点P与点Q都在AB上运动、点P在BC上运动点Q仍在AB上运动、点P和点Q都在BC上运动三种情况，在每种情况下可利用三角函数分别求出我们所需要的值，进而求解．
②在①的基础上，首先①求出函数关系式之后，根据t的取值范围不同函数最大值也不同．

解答：解：（1）当点P运动2秒时，AP=2cm，由∠A=60°，知AE=1，PE=

3

．（2分）
∴S_△APE=

3

2

；（4分）

（2）①当0≤t＜6时，点P与点Q都在AB上运动，如图所示：

设PM与AD交于点G，QN与AD交于点F，
则AQ=t，AF=

t

2

，QF=

3

2

t，
AP=t+2，AG=1+

t

2

，PG=

3

+

3

2

t．
∴此时两平行线截平行四边形ABCD的面积为S=

3

2

t+

3

2

；（8分）
②当6≤t＜8时，点P在BC上运动，点Q仍在AB上运动．如图所示：

设PM与DC交于点G，QN与AD交于点F，则AQ=t，AF=

t

2

，
DF=4-

t

2

，QF=

3

2

t，BP=t-6，CP=10-t，PG=（10-t）

3

，
而BD=4

3

，故此时两平行线截平行四边形ABCD的面积为S=-

5 3

8

t²+10

3

t-34

3

，（10分）
③当8≤t≤10时，点P和点Q都在BC上运动．如图所示：

设PM与DC交于点G，QN与DC交于点F，则CQ=20-2t，QF=（20-2t）

3

，
CP=10-t，PG=（10-t）

3

．
∴此时两平行线截平行四边形ABCD的面积为S=

3 3

2

t2-30

3

t+150

3

．（14分）
故S关于t的函数关系式为

3 2 t+ 3 2 ，(0≤t＜6) - 5 3 8 t2+10 3 t-34 3 ，(6≤ t＜8) 3 3 2 t2-30 3 t+150 3 ，(8≤t≤10)

；

②（附加题）当0≤t＜6时，S的最大值为

7 3

2

，（1分）
当6≤t＜8时，S的最大值为6

3

，（舍去），（2分）
当8≤t≤10时，S的最大值为6

3

，（3分）
所以当t=8时，S有最大值为6

3

．（4分）
（如正确作出函数图象并根据图象得出最大值，同样给4分）

点评：此题解答需数形结合，把函数知识和几何知识紧密联系在一起，难易程度适中．