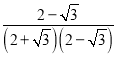Question

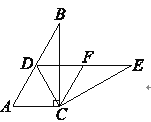
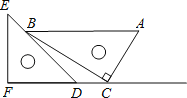
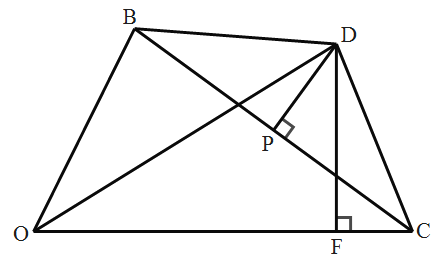
【题目】如图，在△OBC中，边BC的垂直平分线交∠BOC的平分线于点D，连接DB，DC，过点D作DF⊥OC于点F.

(1)若∠BOC＝60°，求∠BDC的度数；

(2)若∠BOC＝，则∠BDC＝ ；（直接写出结果）

(3)直接写出OB，OC，OF之间的数量关系.

Answer 1

【答案】（1）120°；（2）180°－α；（3）OB＋OC＝2OF

【解析】

(1)首先过点D作DE⊥OB于E，易证得△DEB≌△DFC（HL），即可得∠BDC=∠EDF，又由∠EOF+∠EDF=180゜，即可求得答案；

(2)由（1），可求得∠BDC的度数;

(3) OB＋OC＝OE＋OF＝2OF

解：(1)过点D作DE⊥OB，交OB延长线于点E，DF⊥OC于F，

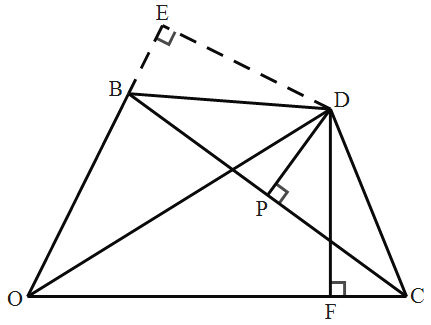
∵OD是∠BOC的平分线，
∴DE=DF，
∵DP是BC的垂直平分线，
∴BD=CD，
在Rt△DEB和Rt△DFC中，
∴△DEB≌△DFC（HL）

∴∠BDE=∠CDF，

∴∠BDC=∠EDF，

∵∠EOF+∠EDF=180゜，

∵∠BOC=60゜，

∴∠BDC=∠EDF=120゜．

（2）∵∠EOF+∠EDF=180゜，

∵∠BOC=α，

∴∠BDC=∠EDF=180゜-α．

故答案为：180゜-α．

（3）由（1）知OB＋OC＝OE＋OF＝2OF