题目内容
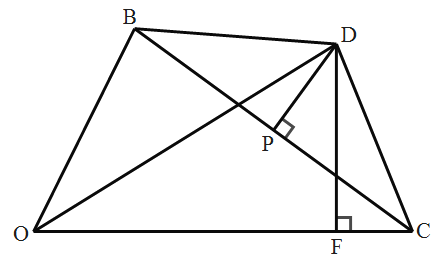
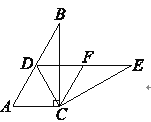
【题目】如图所示,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转,可以得到△DEC.若点D刚好落在AB边上,取DE边的中点F,连接FC,试判断四边形ACFD的形状,并说明理由.
【答案】见解析.
【解析】
由在Rt△ABC 中,∠ACB=90°,∠B=30°,易得△ACD是等边三角形,则可得AC=AD=![]() AB,又由旋转的性质与直角三角形斜边的中线的性质,证得DF=CF=
AB,又由旋转的性质与直角三角形斜边的中线的性质,证得DF=CF=![]() DE,则可得AC=CF=DF=AD,继而证得四边形ACFD是菱形.
DE,则可得AC=CF=DF=AD,继而证得四边形ACFD是菱形.
解:四边形ACFD是菱形.
理由如下:
∵在Rt△ABC中,∠ACB=90°,∠B=30°,
∴∠A=90°-∠B=60°,AC=![]() AB.
AB.
∵将△ABC绕点C按顺时针方向旋转,得到△DEC,
∴CA=CD,AB=DE,∠ACB=∠DCE=90°,
∴△ACD是等边三角形,∴AC=AD.
∵F是DE的中点,∴DF=CF=![]() DE.
DE.
∴AC=CF=DF=AD,
∴四边形ACFD是菱形.

练习册系列答案
相关题目
【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形(如图1),然后拼成一个平行四边形(如图2)。那么通过计算两个图形的阴影部分的面积,可以验证成立的公式是( )
A.a2-b2=(a-b)2 | B.(a+b)2="a+2ab+b" |
C.(a-b)2=a2-2ab+b2 | D.a2-b2=(a-b)(a+b) |