题目内容
【题目】如图,已知等边三角形ABC,点D为线段BC上一点,以线段DB为边向右侧作△DEB,使DE=CD,若∠ADB=m°,∠BDE=(180﹣2m)°,则∠DBE的度数是( )

A.(m﹣60)°B.(180﹣2m)°C.(2m﹣90)°D.(120﹣m)°
【答案】A
【解析】
如图连接AE.证明△ADC≌△ADE(SAS),推出A,D,E,B四点共圆,即可解决问题.
解:如图,连接AE.
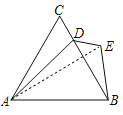
∵△ABC是等边三角形,
∴∠C=∠ABC=60°,
∵∠ADB=m°,∠BDE=(180﹣2m)°,
∴∠ADC=180°﹣m°,∠ADE=180°﹣m°,
∴∠ADC=∠ADE,
∵AD=AD,DC=DE,
∴△ADC≌△ADE(SAS),
∴∠C=∠AED=60°,∠DAC=∠DAE,
∴∠DEA=∠DBA,
∴A,D,E,B四点共圆,
∴∠DBE=∠DAE=∠DAC=(m﹣60)°,
故选:A.

练习册系列答案
相关题目