Question

在正方形ABCD中，点E在BC上，点F在AB上，∠FDE=45°，△DEC按顺时针方向旋转一个角度后成△DGA，如下图所示．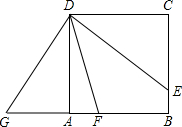
（1）哪一个点是旋转中心旋转角度等于多少？
（2）指出图中的对应线段和对应角；
（3）求∠GDF的度数．

Answer 1

解：（1）D点是旋转中心，旋转角是90°．

（2）对应线段是DE和DG，DC和DA，CE和AG．
对应角是∠CDE和∠ADG，∠C和∠DAG，∠DEC和∠G．

（3）∵∠FDE=45°，∠ADC=90°，
∴∠ADF+∠EDC=90°-45°=45°，
∵∠GDF=∠GDA+∠ADF，∠GDA=∠EDC，
∴∠GDF=∠EDC+∠ADF=45°．
分析：由已知：△DEC按顺时针方向旋转一个角度后成△DGA，观察对应边可得，旋转中心是D点，旋转角为90°；
根据旋转的性质可以得到△DEC≌△DGA，则∠GDA=∠EDC，据此即可求得∠GDF的度数．
点评：本题考查旋转的性质--旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．