��Ŀ����
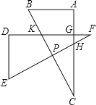
����Ŀ����ͼ��ij��Ϊ�������˹���·��������һ����Ϊ4x��m���Ĺ������ţ���֪���ŵ�б���¶�i=1��0.75��ָ�����Ǧֱ�߶�DE��CF����ˮƽ����AE��BF���ıȣ�����DC��AB��CD=8x��m����
��1������������ܳ�����·����AB�ıȣ�
��2����ij�˴�A�س����������·ֱ�У�A��E��F��B������B�أ�ƽ���ٶ���2.5m/s������ʱ��������BC��CD��DA����A�أ�ƽ���ٶ���1.5m/s�������ȥʱ������12.8s���������·����AB�ij���

���𰸡���1��9��7����2��AB�ij�Ϊ28m.
��������
��1����֤���ı���CDEF�Ǿ��Σ���EF=DC=8x�������¶ȵĶ���ɵ�EA=BF=3x��AD=BC=5x������AB=AE+EF+BF=14x�������ܳ�����·����AB�ı�=18x��14x.(2) �ɣ�1����֪��AB=14x��AD+CD+BC=18x�������⣺![]() ,�ⷽ�̿ɵ�.
,�ⷽ�̿ɵ�.
�⣺��1����DE��AB��CF��AB��
���DEF=��CFE=90�㣬
��DE��CF��
��DC��AB��
���ı���CDEF�Ǿ��Σ�
��EF=DC=8x��
��![]() =
=![]() =
=![]() ��
��
��EA=BF=3x��
��AD=BC=5x��
��AB=AE+EF+BF=14x��
�������ܳ�����·����AB�ı�=18x��14x=9��7��
��2���ɣ�1����֪��AB=14x��AD+CD+BC=18x��
�����⣺![]() =
=![]() ��12.8��
��12.8��
���x=2��
��14x=28��
����·����AB�ij�Ϊ28m.

����Ŀ��Ϊ�μ�ѧУ�ġ��Ұ���ʫ�ʡ�֪ʶ�������������ڰ༶��֯��һ�ι�ʫ��֪ʶ���ԣ�����ȫ��ͬѧ�ķ������÷�ȡ������������Ϊ100�֣�����ͳ�ƣ������Ǹ�����β��Գɼ������IJ�������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ�����������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���ش��������⣺
��� | ���� | Ƶ�� | Ƶ�� |
1 | ��50��x��60 | 9 | 0.18 |
2 | ��60��x��70 | a | b |
3 | ��70��x��80 | 21 | 0.42 |
4 | ��80��x��90 | m | 0.06 |
5 | ��90��x��100 | 2 | n |
��1�����a��b��m��n��ֵ��
��2����ʦ˵���������IJ��Գɼ���ȫ��ͬѧ�ɼ�����λ��������ô�����IJ��Գɼ���ʲô��Χ�ڣ�
��3����Ҫ��С����С���ȼ�λ�ɼ����㣨������80��x��100��Χ��Ϊ���㣩��ͬѧ�����ѡȡ��λ�μӾ��������á��б���������״ͼ�����С����С��ͬʱ��ѡ�еĸ��ʣ���ע����λͬѧ����A��B��C��D����ʾ������С��ΪA��С��ΪB��