题目内容
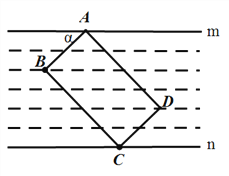
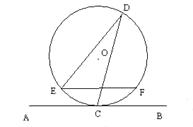
【题目】如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF//AB,若EF=2![]() ,则∠EDC的度数为__________.
,则∠EDC的度数为__________.
【答案】![]()
【解析】
连接OC、OE,由切线的性质知OC⊥AB,而EF∥AB,则OC⊥EF;设OC交EF于M,在Rt△OEM中,根据垂径定理可得到EM的长,OE即⊙O的半径已知,即可求出∠EOM的正弦值,进而可求得∠EOM的度数,由圆周角定理即可得到∠EDC的度数.
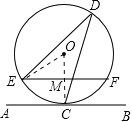
解:连接OE、OC,设OC与EF的交点为M;
∵AB切⊙O于C,
∴OC⊥AB;
∵EF∥AB,
∴OC⊥EF,则EM=MF=![]() ;
;
Rt△OEM中,EM=![]() ,OE=2;
,OE=2;
则sin∠EOM=![]() ,∴∠EOM=60°;
,∴∠EOM=60°;
∴∠EDC=![]() ∠EOM=30°.
∠EOM=30°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目